Your Tree
Christmas Tree Light Calculator
One of Professor Puzzler's Pre-Calculus students posed the following question: If you have a conical Christmas tree, which is ten feet tall, and has a 2.5 foot base radius, how many feet of Christmas lights strands do you need to have in order to wrap around the Christmas tree with the strands 1 foot apart vertically?
I replied, "Welcome to Calculus." But, since he's not a Calculus student, I decided to provide a non-Calculus solution, for anyone who might be trying to figure out how many feet of lights to purchase.
Important Note: This calculator is an approximator. It doesn't take into account that your tree is likely not conical. It also doesn't take into account the sag between branches, or the fact that the branches are not conveniently spaced. All of this adds to the charm of your tree, but the calculator doesn't allow for charm. So if you are using it for anything other than an interesting mathematical exercise (i.e. you really want to know how many strings of lights to buy), make sure you round up generously.
How Does It Work?
The calculator places the Christmas tree into a Cartesian Space (an x, y, z axis), with the center of the base at the point (0,0,0) and the top of the tree at (0,0,h), where h is the height. The beginning of the string of lights is at the point (r,0,0), where r is the radius of the tree's base.
We will split the string of lights into k pieces, where k is the "approximation level" selected. These pieces will all be (for the sake of approximation) straight line segments connecting two end points. These pieces are not all equal in length; they are all equal in rotation. Each piece represents a rotation of 2πR/k, where R (upper case) is the number of revolutions around the tree.
At the base, a revolution of a certain number of degrees will represent a longer segment than that same revolution near the top of the tree. This explains why the pieces are progressively smaller and smaller as we approach the top of the tree.
We can represent the endpoint of the nth segment as another point in space:
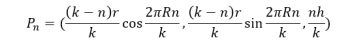
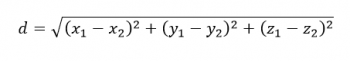
It should be fairly obvious that this estimate is always going to be too small, because our straight line segments actually go through the tree instead of wrapping around it. But the higher our approximation level, the larger the number of pieces, the closer our calculated value will be to the actual value.
And if we could divide it into an infinite number of pieces...
That's where we would have some Calculus!
Merry Christmas!
PS - If you would like to have no revolutions, put zero into the calculator. The string of lights would simply go straight from the edge base to the top, and the length will be (minus a bit of rounding error), the slant height of the cone. This can be calculated using the Pythagorean Theorem: c2 = h2 + r2.
PPS - Another way of approximating (which you can do at home without using any trigonometry, cartesian mapping, or distance formulas) is to treat the lights as a series of concentric rings, instead of as a spiral. The base ring has circumference 2πr. The top ring has a circumference of 0. Since the rings are getting smaller from base to top, at a linear rate, we could reasonably average the two, giving just πr. Now multiply this by R, the number of concentric rings, and you get πrR, which is surprisingly close to the estimate given in the simulation above. I find this especially interesting since this approximating formula does not include the height at all. Makes me wonder...if I took the time to crank out a limit to the approximation...would the h value disappear?

