The Olympus Mons problem is one of my favorite problems to work in class with my Physics students. I wait until after we've covered kinematics, friction, and projectile motion, and then we do a single problem that involves all three of these topics, plus some geometry and trigonometry.

In our problem, we're going to coat the slopes of Olympus Mons with ice, put a student on a sled (or ice skates), and let them slide down the mountain. Our goal is the calculate how far from the base of the mountain they will land.

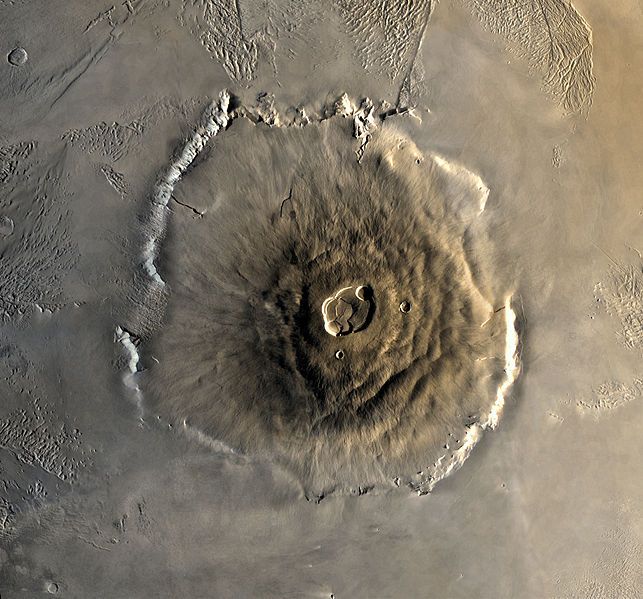
What is Olympus Mons? It is the largest volcano in the solar system, located on Mars. By introduction, I tell my students that Olympus Mons is so big that it's impossible to see the summit from ground level. They find that hard to believe, but they find it even harder to believe when I explain to them that Olympus Mons is so big that, unless you are standing on the mountain, the summit is hidden by the horizon line; it's so big that the summit is further away than the horizon.

Olympus Mons is a shield volcano; it has gently sloping sides formed not by explosive eruptions, but more of a trickling eruption of liquid rock. If you look at the picture above, however, you can see that the gentle slope comes to an abrupt end at the edges of the volcano; this edge is called the escarpment - essentially a cliff. How big is that cliff? It varies in height, but for our purposes, we'll call it 10 km. To give students a point of comparison, the tallest volcano on earth is Ojos del Salado in Argentina, and it is only 6.9 km tall. Imagine that - just the escarpment of Olympus Mons is higher than the largest volcano on earth. This will help students begin to gain a sense for how big this beast is.

What about the caldera? The caldera is about 85 km wide. Before teaching this in your class, you should find a reasonable comparison (Google Earth is very helpful in this regard) to help your students visualize it. I tell my students, "It's about the same as the distance from here to Mount Washington, as the crow flies." Students are now getting an even better understanding of the size.

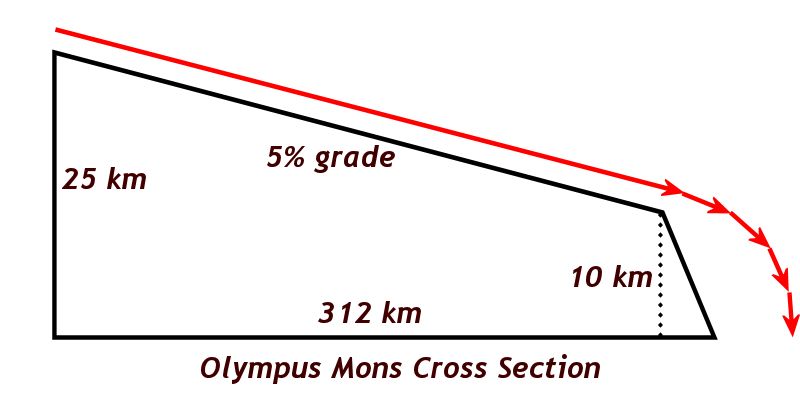
Finally, I give them three more important statistics about the volcano. The diameter at the base is 624 km (again - give them a comparison - I tell my students in Western Maine that 624 km gets them almost all the way to Washington DC); the slope of the non-escarpment surface is 5%; and the height at the caldera is 25 km.

This 5% average slope includes the caldera, which means that, for the sake of doing the geometry, we're going to assume a perfectly even slope all the way from the escarpment to the summit at the center of the caldera. So the diagram would look like this:

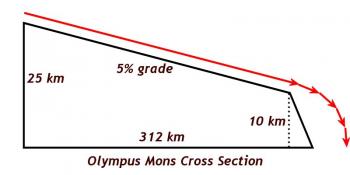
The red line represents the theoretical path of the sled, beginning with a very long downhill ride, and concluding with the sled going airborne as it launches off the escarpment.

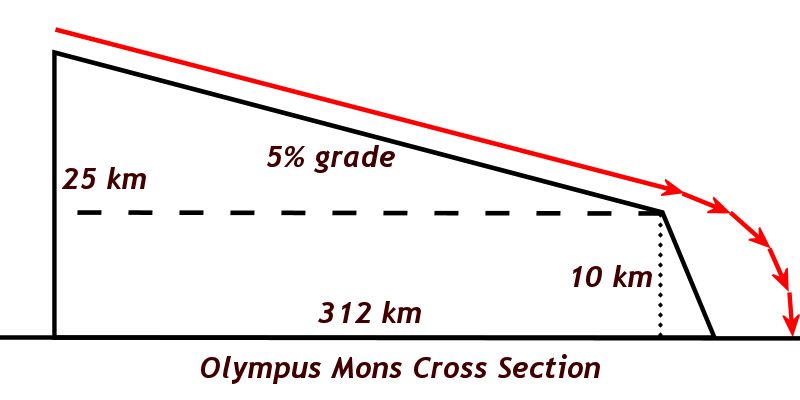
At this point, the students should be given the challenge of determining the various pertinent lengths; how long is the primary slope? How wide is the escarpment? Students will hopefully recognize that drawing a horizontal line from the top of the escarpment to the altitude of the mountain will form a rectangle that allows them to do some calculations.

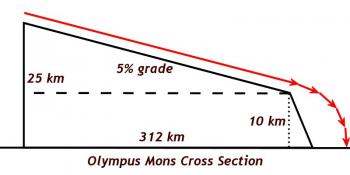
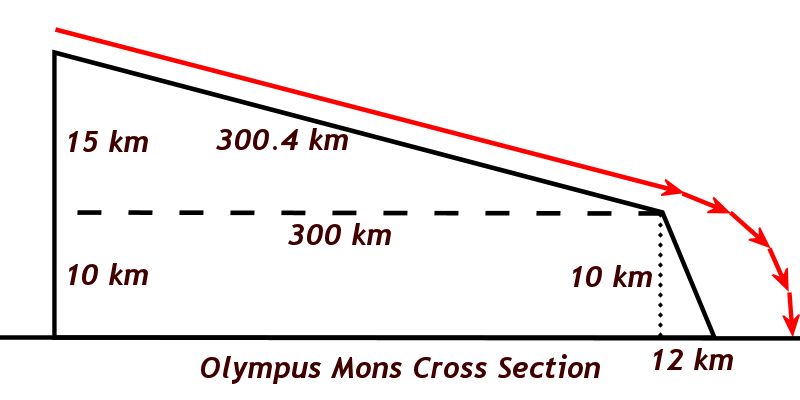
Utilizing what students know about rectangles, and the Pythagorean Theorem, students will be able to determine the following:

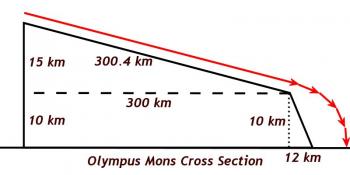
Once we've done all these calculations, we agree that we're going to fly to Mars, flood the surface of the volcano with water, in order to freeze and form a uniform slippery slope with a coefficient of friction of 0.04 (acknowledging that in real life, with our current technology - and funding - these are not possible tasks for us), and then send a student on a wild ride down the slope. 

Now it's just Physics! I usually let the students direct the process of solving the problem, acting as their scribe at the board, and prodding them when then they either get stuck, or head in a wrong direction.

The problem breaks down into two pieces - the sledding (the launch phase), and the flying (the projectile phase).

Here are some things that - in my experience - students may be likely to forget:

• unit conversions
• acceleration due to gravity is not 9.8
  m

  s²
  on Mars. You'll need to provide it: 3.8
  m

  s²
  . I typically don't provide this at the beginning - I wait until they ask for it, and if they don't ask for it, I let them know that they're forgetting something important, and wait for them to figure it out.
• When the sled launches off the edge of the escarpment, it has both a vertical and horizontal velocity, which can be calculated using the slope of the mountain.
• When the horizontal distance from the launch point is calculated, students may forget that the distance from the base of the mountain is 12 km less than that, because of the width of the escarpment.

Every year the students love this problem, and talk about it to underclassmen, so every year that I teach Physics, I have students looking forward to this problem.