Fractal Function

Let F(x) be a non-decreasing function for all x in [0 1], such that

2F(x/3)=F(x) and F(x)+F(1-x)=1

1. Find F(173/1993) and F(1/13).

2. If possible give a general algorithm to find F(x) for any x.

Fractal Function Solution

1. F(173/1993) = 3/16, and F(1/13) = 1/7.

2. Here's the algorithm to find F(x) given x:

1. Express x in base 3.

2. Searching from the left, if any trigit is 1, increase it to 2, and then truncate the base-3 representation after that trigit.

(The result after step 2 is a base-3 number between 0 and 1,inclusive, containing only 0's and 2's.)

3. Replace all the "2" trigits with "1".

4. Re-evaluate the number as a base 2 number. This is F(x).

3 and 4. Yes. Starting with the interval [0,1], and repeatedly dividing it into thirds, we get a dense set of x-values (the endpoints of the successively smaller intervals) for which F(x) is uniquely determined.
Since F is nondecreasing, the values of F between those endpoints must be between the values of F at the endpoints. So F is continuous.

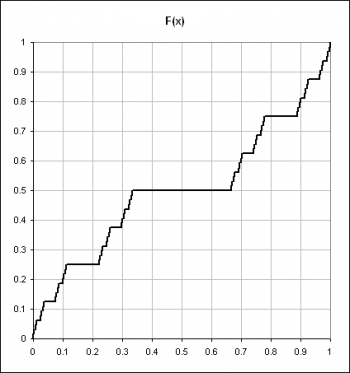
Here's a graph of F:

More about this puzzle:

Proof that F(0)=0: From the definition of F, it follows that if F(x)=y,

then F(x/3)=y/2, and F(1/2)=1/2,

so for any positive integer, k, F(3^-k/2)=2^-k/2. Suppose F(0)=ε, where ε>0. Then an integer, k, exists such that 2^-k/2>ε, and so F(3^-k/2)contradiction.

Corollary: F(1)=1.

Repeatedly dividing the interval into thirds: From facts presented thus far, it follows that F(1/3)=F(2/3)=1/2, dividing the unit interval into thirds. F is constant on the middle third, so there's no need to divide it further, but each of the two other thirds can be divided further into thirds, giving us

F(1/9)=F(2/9)=1/4, and

F(7/9)=F(8/9)=3/4

So you can see that the middle third is a "plateau" after each successive division of an interval. That is, F(x) is constant for all values of x that fall into a middle interval.

Expressing x in base 3 and F(x) in base 2, we see:

F(0.1₃)=F(0.2₃)=0.1₂,

F(0.01₃)=F(0.02₃)=0.01₂,

F(0.21₃)=F(0.22₃)=0.11₂,

F(0.001₃)=F(0.002₃)=0.001₂,

F(0.021₃)=F(0.022₃)=0.011₂,

F(0.201₃)=F(0.202₃)=0.101₂,

F(0.221₃)=F(0.222₃)=0.111₂,

Each digit of the base-3 representation of a number, x, identifies which third of each of the successive divisions the number falls into. If the n'th digit of x (in base 3) is 1, then x falls in the middle third of the unit interval after it has been divided n times. For example, if
x=0.202211202...₃, the fifth digit is 1, and so x falls in the middle third of an interval that is the fifth successive division of the unit interval into thirds. All the numbers between 0.20221₃ and 0.20222₃fall in this interval, so F(x)=F(0.20221₃)=F(0.20222₃). From this, it is clear that upon encountering the first 1 in the base-3 representation of x, the number can be truncated after that trigit, and then the trigit can be changed to 2 without affecting the value of F(x). Then, the value of F(x) is obtained by changing each "2" in x's base-3 representation to "1", and re-interpreting the number as a binary number.

173/1993 is between 0.0021₃ and 0.0022₃, so
F(173/1993) = F(0.0022₃) = 0.0011₂ = 3/16

Repeating Fractions in Base 3: 1/13 is a bit trickier, because in base 3 it's a repeating "decimal" (using the term loosely) that has no 1's. To explore repeating decimals in base 3, I would like to start with a review of an infinite geometric series. Why? If you think about it, you will realize that a repeating decimal in any base is a geometric series. Perhaps you recall that

x^-1 + x^-2 + x^-3 + ... = 1/(x-1)

If not, then refresh your memory this way:

Let S = x^-1 + x^-2 + x^-3 + ...

Then xS = 1 + x^-1 + x^-2 + ...

And xS-S = 1, and then by dividing both sides by x-1,

we see that S = 1/(x-1)

Now, if x is a power of 3 then the sum, S, which equals 1/(x-1), can be expressed very neatly as a repeating fraction. For example, when x=3, 1/(3-1) = 1/2 = 0.111...₃. When x=9, 1/(9-1) = 1/8 = 0.010101...₃. And when x=27, 1/(27-1) = 1/26 = 0.001001001...₃.

What does this have to do with 1/13? Well, 1/13 = 2/26 = 2/(27-1) = 0.002002002...₃.

So F(1/13) = 0.001001001...₂ = 8^-1 + 8^-2 + 8^-3+ ... = 1/(8-1) = 1/7.