One common use of the concepts of uniform circular motion is in the study of orbital motion.  Objects that are orbiting a central body such as satellites around the earth or planets around the sun follow three laws discovered by Kepler.  They can be stated as follows:

1. A radius vector drawn from the sun to a planet sweeps out equal areas in equal times.
2. The planets follow elliptical orbits with the sun at one of the focus points.
3. The ratio of the square of the period and the cube of the average radius is the same for all objects in a given planetary system.

Recall that an ellipse is a figure constructed in such a way that the sum of the two distances from any point on the perimeter of the ellipse to two fixed points, called focus points, is a constant. 

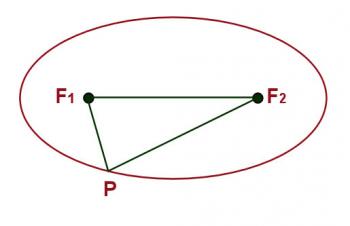
^{Figure 4.3.1}

Refer to figure 4.3.1.  In the diagram f₁and f₂ are the two focus points.  P is any point on the perimeter of the ellipse.  The total distance from f₁ to P and then to f₂ is a constant.  The distance between the focus points is labeled "c" and the line drawn from one end of the ellpise to the other through the focus points is the major axis, "a".  The average radius of the orbit is one‑half the major axis.  The eccentricity of the ellipse is defined as , and can take on any value between 0 and 1.  An eccentricity of 0 means that the two focus points coincide so the figure is a circle.  An eccentricity of 1 means that the focus points are at the very ends of the ellipse giving a straight line.

Figure 4.3.2 il­lustrat­es Kepler­'s first law, the law of areas.  It shows a planet at 4 dif­ferent points in its orbit.  If the time elapsed as the object moves from a to b is the same as that which elapses as the object moves between points c and d then according to the first law the two shaded areas must be equal.  This would indicate that the speed of the planet is greater between points a and b than it is between points b and c.

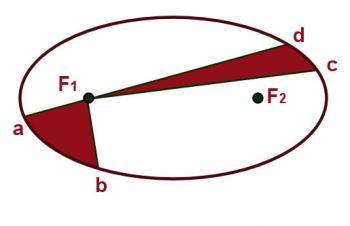
^{Figure 4.3.2}

The point of closest approach to the sun is the perihelion distance  (perigee if for an object orbiting the earth) and the most distant point is called the aphelion (apogee).  It can be shown by application of Kepler's law of areas that the ratio of the aphelion speed to the perihelion speed is the inverse ratio of the the aphelion distance to the perihelion distance.

It can be shown that Kepler's third law is consistent with an inverse square law. That is how Newton was first led to his understanding that the force of gravity was inversely proportional to the square of the separation between two objects.

Much of the math dealing with elliptical orbits is beyond the scope of this course.  We are pretty much limited to comparisons of greatest and smallest speeds for an orbiting object and a comparison of periods and radii for two objects in the same system.  A couple of problems of this type are solved in the sample problem section.  However, if the orbit of an object is nearly circular then the equations for circular motion can be combined with Newton's laws of motion and the law of gravity to calculate many of the orbit parameters.  In many of the problems involving motion around the sun and Kepler's third law it is convenient to measure distances in AU (the average distance between the sun and the earth) and the time in years.  When this is done has the value of 1 since the period of the earth's orbit is 1 year and the average radius of the earth's orbit is 1 AU by definition.  Remember, you may use a value of 1 for the constant only if you are dealing with a member of the solar system and only if you use the correct units.

Sample Problem #1

For the planet Mercury, the perihelion distance has been found to be 45.8 x 10⁶ km, and the aphelion distance about 70.0 x 10⁶ km.  Calculate the eccentricity of the orbit of Mercury and the ratio of the maximum speed to the minimum speed.

Sample Solution #1

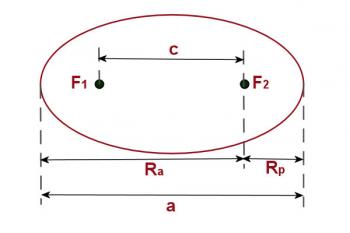
^{Figure 4.3.3}

Examine figure 4.3.3.  Since the focus points are symmetrically placed, it should be apparent that the length of the major axis,a, is r_p + r_a and the distance between the focus points, a, is r_p - r_a.

To find the eccentricity we have:

To find the ratio of the maximum speed to the minimum speed we take the ratio of the maximum distance to the minimum distance.  However, be sure to note that the planet has the maximum speed when it is at the point of closest  approach to the sun.

          = = = 1.53

Sample Problem #2

Halley's comet has a period of 76yrs and its orbit has an ec­centricity of 0.97

1. What is its average distance from the sun.
2. What is its greatest distance from the sun?
3. What is its least distance from the sun?
4. How does its greatest speed compare with its least speed?

Sample Solution #2

Use Kepler's third law to determine R_avg.  Since T is measured in years, we will measure R in AUs so the value of the constant will be 1.  Study Figure 4.3.3 carefully as you work through the problem solution below.

The average radius is half the major axis, therefore the major axis, a is twice R_avg = 35.8 AU.

Since the eccentricity is 0.97 we can find the distance between the focus points, c, by using the definition of ecentricity: 

The closest approach to the sun, Rp, will be 

The furthest from the sun, R_a, will be

The ratio of the greatest to the least speed will be the ratio of the greatest to the least distance or = 64 times as fast.

Sample Problem #3

Use the planetary data in appendix 2 and calculate the speed and period of the moon's orbit around the earth.

Sample Solution #3

Since the moon moves in a nearly circular orbit around the earth we can use Newton's second law and the equations for centripetal acceleration.  The force required to make the moon move in the circular orbit is supplied by the earth‑moon gravitational attraction.

Therefore =

Note that we used the mass of the moon not the earth on the right side of the equation since it is the moon that is being accelerated.  Notice also that the mass of the moon appears in the numerator of the fractions on both sides of the equation so it will cancel out.  The R on the bottom of the fraction on the right will cancel one of the Rs on the bottom on the left.  We obtain:

The easiest way to find the period now is

1.

Find the period of rotation of the earth which would cause objects at the equator to have no apparent weight.

2.

Communications satellites are generally placed in circular orbits above the earth's equator. They are put in orbit at such an altitude that their period of revolution about the earth is the same as the earth's period of rotation. Calculate the altitude necessary for this orbit and the speed of the satellite.

3.

Find the period of a communications satellite in a circular orbit, 22300mi above the earth's surface, given that the radius of the earth is 4000mi, that the period of the moon is 27.3days, and that the orbit of the moon is almost circular with a radius of 239000 mi.

4.

Find the speed and period of an earth satellite traveling at an altitude h=135mi above the surface of the earth. Take the radius of the earth to be 3960mi and the acceleration of gravity at the surface of the earth to be 32.2ft/sec².

5.

Use the distance between the sun and earth and the period of the earth's revolution about the sun (these values are in the appendix) to calculate the mass of the sun.