There are many situations in nature where an object moves around a circular path at a constant speed.  The tip of the blade of a fan or airplane propellor, a fly riding on a longplaying record, or the stone in David's slingshot are all moving with uniform circular motion.  The earth's motion around the sun and the moon's motion around the earth are both good approximations to uniform circular motion as are the motions of many communications satellites.

It is very important to recognize that for an object in uniform circular motion, the speed is constant but not the velocity.  the velocity is not constant because the direction of motion is constantly changing.  Since the velocity is changing the object must have an acceleration if we define acceleration as change in velocity (not speed) divided by the time.  It can be shown that the following equation gives the magnitude of the acceleration for an object in uniform circular motion:

The equation above gives only the magnitude of the acceleration.  The direction of the acceleration vector is always toward the center of the circle.  Whenever working with uniform circular motion it is essential that the directions of the velocity and acceleration vectors be kept in mind.  The velocity vector is always tangent to the circle and the acceleration vector is always radially inward.  The acceleration is often called the central or centripetal acceleration.

Two other quantities are often used in connection with motion in a circle.  They are also used with any periodic motion so you will use them often.  Therefore be sure you learn their definitions well.  The first is the period of the motion.  The period is the amount of time required for one complete revolution in the case of circular motion, or one complete cycle for other cyclic motion.  Since it is really a time, its units will be time units.  The other is the frequency which is defined as the number of revolutions or cycles completed in a unit time, often cycles.  Since it is a number/time, its units are the units of time^-1.  The most common unit of frequency, often used in wave studies, is the Hertz which is 1/sec.  The period and the frequency of a motion are reciprocals  of each other, ie T = and f = .

We would like to be able to relate the centripetal acceleration of an object to its period and frequency.  Consider an object in uniform circular motion of speed V, moving around a circle of radius R with a period T and a frequency f. The distance traveled in one trip around the circle is the circumference , 2 pR Iit requires a time T to make the trip.  Therefore the speed, which is can be found as follows:

 Since T = 1/f  and f= 1/T the previous equation can be written as:

Substitute the values of V in terms of T and f in the equation given above for centripetal acceleration and we obtain 2 more equations for calculating central acceleration.

Since an object moving in a circular path is being constantly ac­celerated it must have a resultant force acting on it.  The force is called the centripetal force and its direction is toward the center of the circle.  The magnitude of the force can be found by using Newton's 2nd law of motion, F = ma, and one of the equations above to calculate the accelera­tion.

Sample Problem #1

A record, 10" in diameter is rotating at 33 1/3 rpm (revolutions per minute) on a turntable.  There are two spots on the record, one is 2" from the center and the other is 4" out.

1. Calculate the frequency and period of the record.
2. Calculate the speed of each spot.
3. Calculate the acceleration of each spot.

Sample Solution #1

1. The frequency is given, 33 1/3 rpm.  In physics we usually would use seconds and would write it differently.  Divide 33 1/3 by 60 to find how many revolutions or cycles are made in one second and write the answer this way:

Since the period is 1/f, the period can be found as follows:

2. To find the speed of a spot on the record use the equation 

3. To find the acceleration either acceleration equation can be used since we have the speed, frequency and period of each spot.

a_c = V²/R = (7.0)2/2 = 24.5 for the inner spot.
a_c = V²/R = (14.0)2/4 = 49 for the outer spot.

Sample Problem #2

David has a giant to kill and his only weapon is a sling.  It consists of two leather thongs 36" long attached to a leather pouch in which David places a small stone.  He spins it in a circular motion which has a radius of 40" making 40 revolutions in 10 seconds and then releases one leather thong sending the projectile toward the giant.  Calculate the speed and central acceleration of the stone in the slingshot.

Sample Solution #2

Very little problem here.  Calculate the speed first as follows:

Sample Problem #3

The coefficient of friction between a car and the road is 0.25.  Calculate the maximum speed at which a 1500 kg car can travel around a curve of radius 100m.

Sample Solution #3

At the maximum possible speed, the force of friction is just sufficient to provide the centripetal acceleration. First we must calculate the possible friction force.

Therefore  

Now calculate the acceleration this force will produce:

Now calculate the speed that will produce this acceleration if the car is moving around a circle of radius 100m.

Actually it is not necessary to give the mass of the car.  It turns out that the mass of the car will cancel out during the calculations.  Redo the problem using M for the mass of the car and you will see that the maximum speed is the same regardless of the mass of the vehicle as long as the coefficient of friction is the same.

Sample Problem #4

A boy swings a pail full of water in a vertical circle so that at the top of the swing it is upside down.  If the radius of the circle is 1 m, calculate the minimum number of swings the pail must make per minute if he is to stay dry.

Sample Solution #4

When the pail is at the top of its swing the water has an acceleration of because of its motion.  It also has an acceleration of 9.8 because of gravity.  If the centripetal acceleration is greater than 9.8 than the boy will have to exert a downward force on the pail to make it move in a circular path.  If the centripetal acceleration of the pail is less than 9.8 than the water will fall out of the pail.  If the centripetal acceleration of the pail is exactly equal to the acceleration of gravity than the water will just stay in the pail with no force on it other than gravity.  Therefore to solve the problem we need to find how fast the boy must move the pail to produce a central acceleration of 9.8 .

If the frequency is 0.5p s than it must be 60 times 0.5 or 30p min^-1.

Sample Problem #5

Roadbeds are frequently tilted or banked on curves so that the road will apply a force toward the center of the curve to help provide the centripetal force necessary to hold a car in a circular path.  Calculate the angle of bank for a roadbed with a radius of 100m if a car is to go around the curve with no friction force.

Sample Solution #5

Examine carefully the following diagram  (Figure 4.2.1) which shows a cross section of the road with a car on it and the forces acting on the car.  If there is to be no friction, the only two forces on the car will be the weight of the car (W) and the normal force of the road against the car (N) as shown.  We need to have the resultant force toward the center of the circle so we will resolve the vectors into vertical and horizontal components as shown.

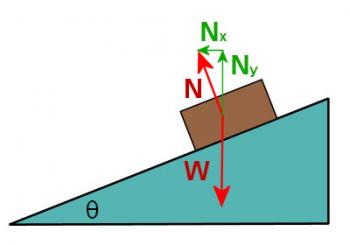
^{Figure 4.2.1} 

Resolve the normal force into vertical and horizontal components.

The car does not accelerate in the vertical direction so

The car does accelerate in the horizontal direction with an acceleration of V2/R, therefore

Combine equations as follows:

 Dividing the first equation by the second we obtain:

Both N and m will cancel showing that the proper angle is the same for cars of any mass.  We obtain:

1.

What is the acceleration of a point on the rim of a flywheel 0.90m in diameter, turning at the rate of 1200rev/hr?

2.

A stone of mass 100g is whirled in a horizontal circle at the end of a cord 100cm long. If the tension in the cord is 2.5N, what is the speed of the stone?

3.

What is the centripetal force required to cause a 3200‑lb car to go around a curve of 880ft radius at a speed of 60mph.

4.

The outside curve on a highway forms an arc whose radius is 150ft. If the road surface is 30ft wide and its outer edge is 4ft higher than the inner edge, for what speed is it ideally banked?

5.

An unbanked curve has a radius of 80.0m. What is the maximum speed at which a car can make the turn if the coefficient of friction is 0.81?

6.

A pendulum has a bob with a mass of 1kg and a string length of 2.0m. The bob is set into motion in such a way as to make a circular path of radius 0.25m. Calculate the speed of the bob, the period of the motion, and the tension in the string.

7.

A car on a country road in Maine passes over an old fashioned hump‑backed bridge. The center of gravity of the car follows the arc of a circle of radius 88ft. Assuming that the car has a weight of 2tons, find the force exerted by the car on the road at the highest point of the bridge if the car is traveling at 30mph. At what speed will the car lose contact with the road?

8.

A ride at an amusement park consists of a horizontal circular platform surrounded by a metal wall. The platform is 10m in diameter and rotates around a vertical axis through its center. The riders stand with their backs to the outside wall and as the speed of rotation of the platform increases the wall presses against their backs. If the speed is high enough the friction force between the riders and the wall becomes great enough to hold them in place if the floor is dropped away from their feet. Assume that the coefficient of friction between their backs and the wall is 0.4. Calculate the minimum number of revolutions per minute that the ride can turn and hold the riders up and show that it is the same for all riders.