Introduction

Kinematics is that branch of physics that deals with a description of motion.  It makes no effort to explain the causes of motion, indeed the causes cannot be studied meaningfully until the motion can be correctly described.  In this chapter, motion along a straight line will be studied.  A good understanding of the principles in this chapter is necessary before attempting to study either the causes of motion or more complex motions.

                                    
Displacement and Position

Before attempting to describe the motion of an object it is necessary to be able to describe its position.  This is usually done by reference to a Cartesian coordinate system, either a two or three dimensional one.  For the type of motion studied in this chapter it is only necessary to refer to a number line consisting of an origin, the set of positive numbers running one way and the negative numbers going the other.  If the object whose motion is being studied is moving on the surface of the earth, the number line will be a horizontal one.  If the object is  moving up or down the line will be a vertical one.  The conventional number line used in algebra has positive numbers to the right of the origin and negative numbers on the left.  When a vertical line is used it is conventional to place positive numbers above the origin.  However, in physics the sign conventions are often reversed if by doing so a problem is simplified. Examples of where this is convenient will be given later.  It is usually best to take the origin of the number line at the point where the motion starts. Often the number line (usually called the reference system) is not explicitly referred to. In this case the problem solver must have a clear picture of the reference system being used in his or her mind. 

It is necessary to make a clear distinction between the terms position and displacement.  Position refers to where an object is on the reference system, while displacement refers to the change in position if an object is moved.  Refer to Figure 1.1.1.

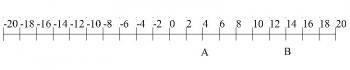
^{Figure 1.1.1}

The position of point A is +4 and the position of point B is +14.  If an object is moved from A to B its displacement is +10.  If an object is moved from point B to point A its displacement is -10.  The displacement can be written a X= -10.  The symbol Δ, is the Greek letter "delta" and stands for "the change in . . . "  Be sure to watch signs, both on your values of position, X, and displacement,  ΔX.  Frequently you will be measuring displacement from the origin in which case ΔX=X, but it is best to still refer to it in your equations as ΔX.

Time Intervals

In order to describe motion it will be necessary to measure time.  Time is usually measured in seconds.   It is necessary to distinguish between time, t, and a time interval, Δt.  Time can refer to the time of day or the time elapsed since the start of a certain clock.  The time interval,  Δt, refers to the time elapsed between two events. If we start our clock when the motion starts,  Δt will be equal to t. However, the two quantities are not always equal.

Average Speed

There are a number of important facts to note in relation to the use of this equation.  If an object is moving at a constant speed, then the average speed is equal to the actual speed at any instant during the interval.  If the object is not moving at a constant speed, the average speed may bear little resemblance to the actual speed at points during its motion.  If the speed of the object is changing at a constant rate the average speed is equal to the actual speed at the midpoint of the motion.  If the value of the time interval is very short, the average speed is close to the actual speed at each point of the interval.  As the time interval approaches zero the ratio approaches a limit which is defined as the instantaneous speed at that point.

To demonstrate the limitations of eqn 1 consider the following problem:

A family on vacation travels 240 miles in 6 hours.  Find their location and speed 3 hours after leaving home.

By dividing 240 miles by 6 hours we obtain an average speed of 40 mph.  We might then be tempted to answer the problem by saying that after three hours they are 120 miles from home (40 mph times 3 hrs) moving at a speed of 40 mph.  However, these answers  are not necessarily correct.  The family undoubtedly did not travel at a constant speed for the entire trip.  Three hours into the trip  they may be  stopped at McDonald's for lunch in which case their speed would be zero.  Depending on traffic conditions they might have traveled more or less than one half of the trip.  There is no way to answer the questions from the information given.