We have studied Newton's second law of motion, which states that if the vector sum of the forces acting on a body is zero, the body will remain in equilibrium. However, a more carefull consideration of the problem reveals that there is an exception of sorts to this rule, and we need to modify the second law in order to make it fit all situations.

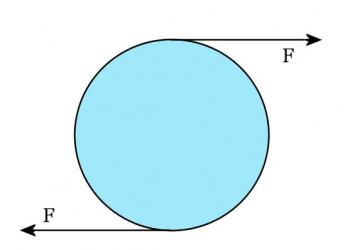
^{Figure 6.2.1}

Consider the following situation illustrated in Figure 6.2.1. A large disk-shaped block of dry ice is placed on a smooth horizontal surface. Two equal and opposite forces are applied to the disk as shown in the diagram. Clearly the forces are balanced, but the disk will not remain motionless. It will begin to rotate about an axis through the center of the disk.

Thus we see that we need to divide the motion of an object into two types: the translational motion of the object through space and a rotation of the object around some axis. If the vector sum of the forces on the object is zero, the body will remain in translational equilibrium, but an additional condition must be met if it is to remain in rotational equilibrium. An object is said to be in rotational equilibrium if its angular velocity remains constant.

We now introduce the concept of Torques. A torque is defined as the product of the distance from the point of application of a froce to some axis and the component of force which is perpendicular to this radius arm. We then add a statement to Newton's second law as follows:

"If the sum of the clockwise torques around any axis of a body is equal to the sum of the counter-clockwise torques around the same axis, the body will be in rotational equilibrium. A body which is in rotational equilibrium does not rotate, or rotates with a constant angular velocity."

In most cases where non-concurrent forces are studied, a major force acting on an object is its own weight. Thus it is necessary to find a way to consider the weight of the object in rotational problems. We define the center of gravity of an object as the point at which it will balance. Since the object balances at this point, it is apparent that the object's weight produces no torque about that point. Thus, for the purpose of computing torques, we may assume that the weight of the object is concentrated at the object's center of gravity.

There are are many situations where a study of torques provides useful information. In general, any time an object has forces acting on it which are not concurrent, i.e. they do not all pass through a common point, torques must be considered. Many times the body under study does not have an obvious axis of rotation. For example, one might wish to calculate the load supported by each abutment at the end of a bridge with the weight and length of the bridge given along with the weight and position of any vehicles on it. To solve the problem, assume that one of the abutments is an axis around which the torques produces by the weight of the bridge and the vehicles on it would cause the bridge to rotate if they were not balanced by an equal and opposite torque produced by the upward force from the other abutment.

When solving torque problems it is essential that you draw a good diagram showing all the forces acting on an object, including the object's own weight acting at the object's center of gravity, as well as the point of application of each force. Equations can then be written in which the torques causing a rotation in one direction are balanced against the torques producing rotation in the opposite. A variety of solved problems requiring the use of torques are provided. Study them carefully.

Vectors in Rotational Motion

Suppose that there is a disk in rotation about an axis through its center with an angular velocity ω. Clearly there is a direction involved. It would be possible to specify the direction of the axis and then state whether the rotation is clockwise or counter-clockwise about that axis. However, it is desirable to be able to specify a single direction and thus clearly describe the rotation of the disk. The convention used is as follows. Imagine an axis through the disk and perpendicular to it extending out each side beyond the disk, as shown in Figure 6.2.2. Imagine that you grasp the axis with your right hand with your fingers wrapped about the axis in the direction of rotation of the disk, and your thumb extended along the axis as shown. By definition, the angular velocity vector points in the direction of your thumb as shown by the arrow. According to this convention, the angular velocity of the earth is north.

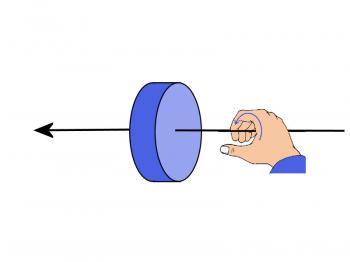
^{Figure 6.2.2}

Torque is defined as the product of a force and a distance, both of which are vectors. Torque can also be a vector if we multiply the force and distance with a vector or cross product. Refer back to the section in chapter 3 on multiplication of vectors to review how to find the direction of the vector. Remember that vector multiplication is not commutative and we will obtain different direction for the product vector if we find FxR than if we find RxF. The correct and complete definition of torque is:

Sample Problem #1

A 1000 N sign mounted on the side of a building is suspended from a horizontal rigid rod 1.5 m long, which is supported at one end by the building, and at the other by a steel cable which makes an angle of 40º with the horizontal. The sign is hung from the rod at a point 1 m from the wall. The end attached to the wall is free to pivot. Calculate the force exerted on the rod by the wall and the force in the cable, if the weight of the rod and the weight of the cable are neglected. See figure 6.2.3.

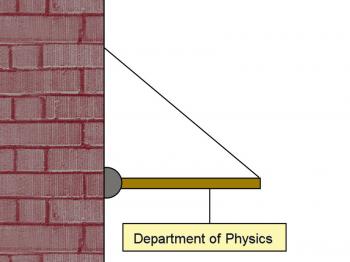
^{Figure 6.2.3}

Sample Solution #1

In a problem such as this it is essential to draw a clear diagram with all information given shown on the diagram. Study figure 6.2.3b carefully.

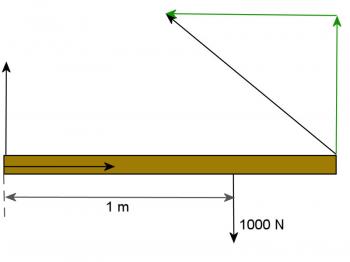
^{Figure 6.2.3b}

Note that all distances and known forces are shown in the diagram. Since the forces do not all meet at a point, it will be necessary to consider torques in order to solve the problem. Sketch a second diagram showing just the object under consideration, in this case the steel rod, and the forces acting on it. Also show any distances that are known. Indicate with arrows any unknown forces and identify them with letters. In the problem here, the force in the cable is pulling the rod toward the wall. Therefore, if the rod is to remain in equilibrium, the wall must be pushing out with some force, F₁ in the diagram. It is also necessary for the wall to exert an upward force on the rod to hold the sign up. This force is labeled F₂. Finally there is a tension force in the cable, labeled T. The tension in the cable has been broken up into vertical and horizontal components, T_x, which is Tcos40º, and T_y, which is Tsin40º.

If the bar is to remain in equilibrium, then the sum of the vertical forces must be zero, and the sum of the horizontal forces must be zero. Write equations expressing this as shown below.

Rewrite these in terms of T and the angle.

Since there are three unknowns and only two equations, it will be necessary to write a third equation. We will obtain the additional equation by considering torques and requiring the object to remain in rotational equilibrium.

First, select some point as a pivot. This point can be any point, even some point not on the object if you wish. However, you can often make simpler equations by careful choice of the pivot point. Keep in mind that a torque is force times distance from the pivot to the point of application of the force. If you select a point through which a force passes as the pivot, then the torque produced by that force will be zero. In this problem, the most logical point to select as the pivot is the end of the bar supported by the wall. Now write an equation setting the sum of the torques rotating the bar one way equal to the torques rotating the bar the opposite way:

This gave us more than we expected! The only unknown appearing in the equation is T, so we were able to find T using this equation, without the necessity of solving a system of equations. If we had chosen a different point as pivot, this might not have happened.

We will have to find F₁ and F₂. There are several ways of doing this. One is to use the value of T computed above and the two equations we first wrote for this problem. Another would be to write a second torque equation using the pivot point as the point at which the cable is attached as shown below:

It is a good idea to check our work at this point. The total upward force is F₁ plus the upward component of T, or Tsin40º. This total upward force should be equal to the weight of the sign. You should demonstrate that the sum of these two forces in fact is equal to 1000 N.

To find the value of F₂, use the equation

You might try to select a different point as a pivot to see if you get the same answers. Remember that the point selected does not need to be a physical pivot; it is simply a mathematical point around which to take torques. It could be located 2 m from the wall and 1 m above the bar. This would make the mathematics more difficult but the answers would be the same.

Sample Problem #2

A log 6 m long weighs 5000 N. It takes a force of 3000 N to lift the heavy end. Locate the center of gravity of the log.

Sample Solution #2

Start by drawing a diagram. Show the weight as a downward force nearer the heavy end than the light, and a distance R from the light end. Show an upward force of 3000 N at the heavy end. See Figure 6.2.4.

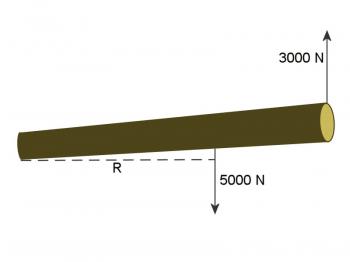
^{Figure 6.2.4}

This is an easy problem. Take the left end as the pivot. Set the torque produced by the weight equal to the torque applied to lift the right end.

Sample Problem #3

A plank, 6 m long and weighing 400 N, has its center of gravity 4 m from one end. It is supported near each end and two painters are standing on it. One weighs 500 N, and is at the center. The other weighs 350 N, and is standing 1 m from the light end. Calculate the force exerted by each support.

Sample Solution #3

Again, start by drawing a diagram showing all forces and distances. See Figure 6.2.5.

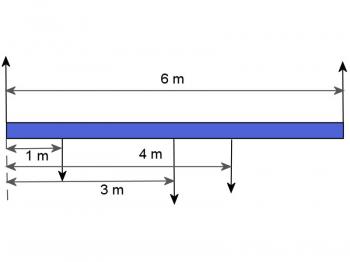
^{Figure 6.2.5}

Once the diagram is drawn correctly, the problem is quite easy. Take torques around the left end as follows:

Solve this equation to obtain F_B = 575 N.

There are two ways to calculate the other force. You can add the weight of the plank and the two painters and subtract the upward force calculated above from the total. The difference is the force supplied by the other end.

Another, possibly better way, is to take torques around the right hand end of the plank. When doing so be sure to find correctly the distances from the right end to each force by subtracting the distance shown from 6 m.

Solve to obtain F_A = 675 N.

You can then check your work by adding the two upward forces and see if they equal the total downward force.

1.

Where should a uniform board 100 cm long be supported in order to balance a 10 g mass placed at one end, a 60 g mass on the other end, and a 40 g mass 30 cm from the 10 g mass?

2.

In the question above, what is the magnitude of the supporting force?

3.

Two men lift the ends of a uniform beam of length 20 ft and weighing 200 pounds. Both men are of the same height so the beam is carried horizontally. One of the men is much stronger than the other and wishes to bear 50% more of the weight than his co-worker. How far from the end of the beam should he lift?

4.

A uniform wooden beam of length 20 ft and weight 200 pounds is lying on the floor. Jack raises one end of it until the beam has a 30 degree angle of inclination. He holds it in this position by exerting a force at right angles to the beam while waiting for Jill to lift the other end. What is the magnitude of the force he exerts?

5.

A rope is supporting a 200 pound uniform beam which is 20 ft long. One end of the beam is hinged at a wall and the other end of supports a 1.0 ton load. The rope is attached to the end of the beam and makes an angle of 30 degrees with the horizontal beam. What is the tension in the rope?

6.

In the previous question, find the force at the hinge.

7.

A non-uniform bar weighing 1000 N is suspended horizontally at rest by two ropes attached to opposite ends of the bar. The two ropes make angles of 30 degrees and 60 degrees with the vertical. If the length of the bar is 10 m, what is the tension in each rope?

8.

In the problem above, What is the distance from the light end of the bar to the center of gravity?

9.

A 20 foot long ladder is placed against a vertical frictionless wall with a 53 degree angle of inclination. The ground is not frictionless. The ladder is in equilibrium. Its weight is 80 lb, and its center of gravity is at its center. What are the magnitudes and directions of the forces exerted by the wall and ground on the ladder?

10.

The front wheels of an empty pickup truck are on a scale, and the scale reads 3500 lb. The the rear wheels are placed on the scale, and the scale reads 2500 lb. The pickup's wheel-base is 14.0 ft. How far from the rear axle is the center of gravity?

11.

A 1200 N cubical box is 2 meters on a side. It rests horizontally on the floor. A small obstacle is along one edge, which keeps the box from sliding. In order to overturn the box most easily, where should I push, and what is the minimum force I must apply?