Frequently we encounter a type of motion, called harmonic motion, where an object moves back and forth along a line. One kind of harmonic motion, called simple harmonic motion (SHM), is best thought of as a special case of rotational motion, so will be introduced here.

Consider a flat disk resting on a turntable with a small object attached to the disk so that it protrudes above the surface of the disk. Now place a screen near the disk and shine a light on the disk so that a shadow of the object is thrown on the screen, and start the disk in rotation. You will see the shadow move back and forth on the screen. If you study the motion for a moment, you will realize that the object stops at one end, starts moving toward the other end of its motion, reaches its maximum speed at the midpoint of its motion, begins to slow down, and stops at the other end. It then moves in the same manner in the other direction.

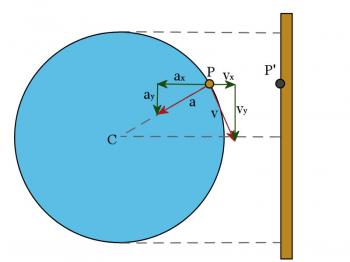
^{Figure 6.4.1}

To analyze the motion you need a good sketch of the circular motion which produces it. Study Figure 6.4.1. At the left is a diagram of the motion of the object in a circular path and at the right is a diagram of the motion of the shadow. As with any periodic motion, we define the period, T, as the time for one complete cycle and the frequency, f, as the number of cycles completed per second. It should be clear to you that the periods and frequencies of the two motions are the same since it takes exactly the same time for the disk to complete one complete revolution as it takes for the shadow to move from top to bottom and back again. We also will define the amplitude of the SHM as the distance from either end to the midpoint of the motion. This is the same as the radius of the associated circular motion.

Consider the circular motion first. The speed of the object will be given by and the acceleration will be . Both the velocity and the acceleration are vectors. The velocity vector is always tangent to the circle, and the acceleration vector is always pointed toward the center of the circle. At a particular instant of time, the object is in the position labeled P in Figure 4A, and the shadow is at the point labeled P' in Figure 4B. At this instant the radius line drawn from the center of the circle to point P makes an angle θ with the horizontal as shown. The value of θ can be found by sin^-1() where x is the displacement of the shadow from the equilibrium point as shown in Figure 4B.

Now let us add velocity and acceleration vectors to the diagram as shown (labeled V and a). The motion of the shadow will be the component of the motion of the object which is either up or down. Thus the velocity of the shadow at any instant will be the vertical component of the velocity of the object at that instant, and likewise for the acceleration. The vertical (y) and horizontal (x) components of the velocity and acceleration vectors are shown as dotted lines. To find the velocity of the shadow at the point P', we need to find the vertical component of the velocity of the object when it is at P. This will be equal to 2pRcosθ. The acceleration of the shadow at P' will be ()sinθ. Be very careful to indicate directions for the velocity and acceleration vectors. If the shadow is moving up at P' as shown in the diagram, then its velocity is up and its acceleration is down. This corresponds to what we know; the object is moving up and slowing down. If the shadow is moving down at point P', then you should be able to sketch the proper position of the object in the circular motion and show that the vertical components of both the velocity and acceleration will be down.

Note that at point P the position of the shadow is given by Rsinθ, and the acceleration is given by -()sinθ. By Newton's second law, F = ma. Therefore, F = -m()sinθ. Thus, F ∝ -sinθ and y ∝ -sinθ, so F must be proportional to the negative of the displacement, or 

From this we see that we will get simple harmonic motion whenever the force is proportional to the negative of the displacement. The negative sign simply means that the force will be in the opposite direction from the displacement. This also means that the force will always be directed toward the equilibrium point. A weight bouncing up and down on the end of a spring closely approximates this condition and there are many other examples of this motion in Physics.

As with the other material, you will understand this better after you work through the solved problems.

Sample Problem #1

A weight on the end of a spring is displaced 10 cm from its equilibrium position and released. It then oscillates up and down, making 10 vibrations each minute. Calculate:

1. the maximum speed of the object
2. the maximum acceleration
3. the speed and acceleration of the weight when it is 5 cm above the equilibrium point and is moving down.

Sample Solution #1

In this kind of problem, you need to keep in mind two related motions: the motion of the weight, which is simple harmonic motion, and the circular motion of an object which will duplicate the SHM when viewed on edge. First draw two diagrams. One of the object in SHM and the other of the circular motion which corresponds to it. Refer to Figure 6.4.1 above. Then list all the known variables, keeping in mind that some variables have the same value for both motions.

1. The maximum velocity of the object will be as it passes through the midpoint of its motion and will be equal to the speed of the object in circular motion. To find the speed of the motion of the object in the reference circle:

2.  The maximum acceleration of the object in SHM will be at either end point, and will be equal to the central acceleration of the object moving around the reference circle. Thus:

3.  The last part is slightly more difficult. First we must locate the position of the object in the circular motion which corresponds to the position of the object in SHM. Refer to the diagram above. We are asked to find the velocity and acceleration of the object when it is at the position labeled P. The position of the object in circular motion which corresponds to this position is labeled P'. Since the object is 5 cm above the equilibrium position, it should be clear that the angle θ is sin^-1() = 30º.

Now we draw the vectors representing the velocity and acceleration of the object in circular motion. Resolve them into horizontal and vertical components, as shown in the figure. Finally, use the known value of the angle θ to find the vertical components of these vectors. The vertical components are the velocity and acceleration of the object in SHM. Thus:

And

All problems in SHM can be handled this way. Just be sure to draw a careful and accurate diagram. Draw the diagram large enough so that all the vectors, the appropriate angles, and the components can be clearly shown.

Sample Problem #2

A simple pendulum (a point mass on the end of a rigid, massless rod) moving through small angles executes a motion that is very nearly SHM. The pendulum's period given by the following equation:  

For this formula, l is the length of the pendulum and a_g is the acceleration of gravity.  

A simple pendulum has a period of 2.40 sec at a place where a_g= 9.8 .  What is the value of a_g at another place on the earth's surface where this pendulum has a period 2.41 sec?

Sample Solution #2

The period is 2.40 s, when a_g = 9.8 , so we know:

Therefore, l = 1.43 m.

We now can use this length, along with the new period, to determine a_g at the other location on the earth's surface:

Therefore, a_g = 9.65

1.

A thin piece of metal is clamped in a vise and the other end is given a to and fro vibration. The motion of the free end is simple harmonic motion. If the frequency of vibration is 10/sec and the amplitude is 4 mm, what is the velocity of the free end when its displacement is 2 mm from the equilibrium position?

2.

An object with mass m moves with simple harmonic motion, with period T and amplitude A. There is no force acting on the particle at time t=0. what is the force at time t=?

3.

An 8 kg object has simple harmonic motion of amplitude 1.0 m and period 3.0 sec. What is the force acting on the body 5.25 sec after it leaves one end of the path?

4.

What is the speed of the object in the problem above at the given moment in time?

5.

What is the average speed between the end points of the path of the object described above?

6.

Compute the period of a vibrating particle, if it has an acceleration of 64 cm/s² when its displacement is 16 cm.

7.

A 49 g body's motion is SHM. The body makes 4 complete vibrations per second. Compute the acceleration and the force acting on the body when displaced 2 cm from the center of its path.

8.

A pendulum has a period of 1 sec in London, where a_g=32.200 . But then the pendulum is taken to Paris, and it loses 20 . What is the value of a_g in Paris?

9.

What is the length of a simple pendulum if it has a period of 1 sec at the surface of the earth?