The con­cept of vectors has been introduced by using examples of displace­ment vectors.  These are probably the easiest type of vector problems because they are the easiest to visualize.   There are two other types of vector problems that will be studied in this chapter, velocity and force.  Techniques for dealing with velocity and force problems will be developed in the solved problem section.  

There are two principal types of force problems: 

1. Equilibrium problems where it is known that an object is in equilibrium and some of the forces are given.  The student then must determine the necessary missing force(s) to produce equilibrium.  
2. Non-equilibrium problems where all forces are given and it is necessary to combine them to see if the object is in equilibrium, and to determine the magnitude of the unbalanced force, if any, in order to find the object's acceleration.  

Non-Equilibrium Vector Problems

Most problems involving addition of velocity  vectors are quite straight forward.  The typical problem will have some object, a boat or plane for example, which has a known velocity through some medium, air or water, which is itself in motion at a known speed.  The resultant velocity of the object will be the vector sum of the two velocities.  Sketch a good vector diagram before trying to do any calculations.  It is not necessary to construct it to scale but it should be sketched so distances and angles are in approximately the correct proportion to each other.  In these types of problems it is usually more logical to sketch the diagram so that a second vector starts at the point of the first.  If the two vectors are at right angles to each other the problem can be solved easily by application of the Pythagorean theorem to find the magnitude of the unknown vector and by use of trigonometry to find any unknown angles.  If the vectors are not at right angles to each other, draw the diagram as before and then resolve one of the vectors into components which are parallel and perpendicular to the other vector.  Both types of problems are illustrated below.

Sample Problem #1

A boat operator in a boat which can travel 15m/sec in still water tries to cross a river which is flowing at 5m/sec by pointing the boat directly across the river.  What will be the resultant velocity of the boat?

Sample Solution #1

The first step is to draw a vector diagram as is shown in Figure 3.4.1.   In this diagra­m, V_B represents the velocity of the boat, V_W  rep­resents the vel­ocity of the water and R rep­r­esents the re­su­ltant veloc­it­y.  The student should be able to show that the resultant velocity is 15.8m/sec at an angle of 18.4º down river.

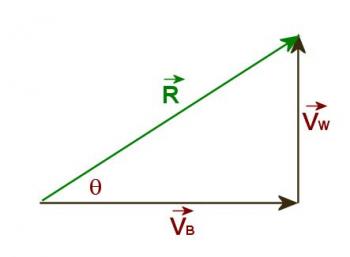
^{Figure 3.4.1}

Sample Problem #2

An airplane can fly at 200mph in still air and wishes to fly due west.  There is a wind of 25mph blowing from the south west (exactly half way between south and west).  Determine the direction the pilot must point the plane in order to fly in the desired direction and determine the resultant speed of the plane.

Sample Solution #2

See Figure 3.4.2.  The direc­tions have been set up as they would be on a map, with west on the left and north at the top of the diagram.  An east­west line is drawn for reference.  Since the bearing of the plane is unknown at this point the vector representing the plane's velocity is drawn at a convenient angle south of west. However, the wind is sketch­ed at ap­proximately a 45º angle with the east‑west line.  Also note that the end of the wind vector must lie on the east‑west line since the plane must end up flying west.  The vectors labeled P, W and R  stand for the velocity of the plane, veloc­ity of the wind, and resul­tant velocity respectively.  Θ is the re­quired bearing of the plane which is un­known.

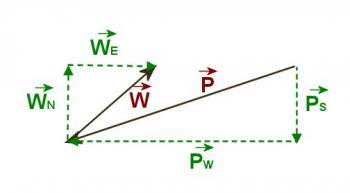
Figure 3.4.2

Since the vectors are not perpen­dicular to each other it is necessary to pick a con­venient set of axes and resolve all the vectors into components parallel to the axes.  In this case it seems logical to resolve all vectors into components which are north and east.  These are represented by the dotted lines in the diagram and have sub­scripts N, S,and  E to denote which axis they are parallel to.

To find the various vector components proceed as follows:

The final velocity of the plane must be west so the north component of the wind must equal the south component of the plane.

The resultant velocity is the west component of the plane's velocity minus the east component of the wind's velocity.

Sample Problem #3

A boat has a constant velocity of 10m/sec east when it encounters a steady wind that blows for 10 seconds.  During that 10 seconds the boat has a constant acceleration of 0.3m/sec2 at an angle of 25O N of E.  What will be the velocity of the boat at the end of the 10 seconds?

Sample Solution #3

By definition  a = ΔV/Δt, therefore   ΔV = 3m/sec at 20º N of E.  If this value of  ΔV is added to the initial velocity the resultant will be the final velocity.  See Figure 3.4.3 below.  In order to add the two vectors it is easiest to break the vector representing  ΔV into north and east components.  These are represented by the dotted lines.

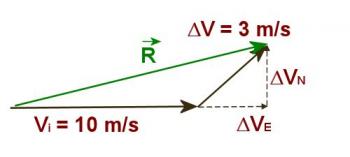
^{Figure 3.4.3}

Calculate the east and north components of V as follows:

The east and north components of the final velocity are therefore:

Use the Pythagorean theorem and trigonometry to find that the final speed, R, is 12.8m/s at an angle of 4.5º N of E.

Equilibrium Problems

One of the most difficult parts of these problems is in the identification of all forces acting on an object. Remember that you want ALL forces which act on the object, you are not interested in any forces the object exerts on its surroundings.  Therefore be sure to draw any vectors in the correct direction.  With the exception of field forces (gravitational, electrical and magnetic) all forces will be applied to an object at the point of contact with another object.  Usually the magnitudes or directions of one or two forces will be unknown.  In these cases estimate the correct position and approximate direction of any unknown force and represent any unknown lengths or angles by variables.  At the present time all forces will be concurrent, that is if the force vectors are extended backward they will all meet at a common point.  Problems involving non‑concurrent forces require the notion of torques and rotational equilibrium and will be studied at a later time.

In setting up vector diagrams for these problems it is usually best to draw all vectors originating from a common point.  Then select a convenient set of perpendicular axes and resolve all vectors into components parallel to these axes. In most cases the best set of axes will be horizontal and vertical.  However be on the alert for situations where a different selection of axes will simplify the problem.  For example, with an object resting on an inclined surface the best choice of axes is parallel and perpendicular to the incline rather than vertical and horizontal.  After finding the components of the vectors add all components parallel to each set of axes to determine the x and y components of the resultant.  Since the object is known to be in equilibrium the sum of the x components and the sum of the y components must both be zero.  This will provide two equations and allow you to solve for as many as two unknowns, either forces or angles.

The variety of problems involving the addition of forces is almost endless so it is impossible to give examples of every type of problem.  Study the approach to each problem solved below and when you encounter a new type of problem try to apply the same techniques.

Sample Problem #4

A box with a mass of 10kg rests on a frictionless surface which makes an angle of 25O with the horizontal.  How large a force must be applied to the box, parallel to the incline to hold the box stationary on the incline?

Sample Solution #4

 

Sketch a diagram of the box and incline as shown in figure 3.4.4.

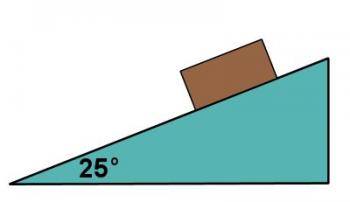
^{Figure 3.4.4}

Then sketch a second diagram showing just the forces acting on the box as shown in Figure 3.4.5.  

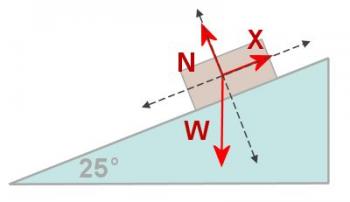
^{Figure 3.4.5}

W  represents the weight of the box (not its mass), X  represents the unknown applied force, and N represents the normal force applied by the surface on the box.  To find the weight remember that 

 Draw in a convenient set of axes and draw the forces in.  In this case the best axes are parallel and perpendicular to the surface of the incline and are shown in Figure 3.4.5.  Finally sketch a vector diagram and resolve any vector which does not lie on one of the axes into components parallel to one of the two axes (figure 3.4.6).  In this case the only vector which needs to be broken into components is W and its components are shown by dashed lines.

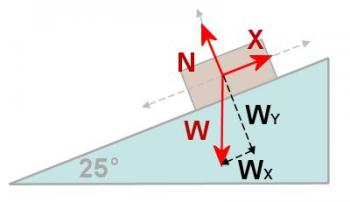
^{Figure 3.4.6}

Now calculate the value of W_x and W_y as follows:

Wite an equation setting the total forces in the positive X direction equal to the total forces in the negative X direction.  Do the same for the forces in the Y direction.

In this case you are done at this point.  The required answer is the force parallel to the incline which is X = 41.4 N.  In some cases you will obtain a set of simultaneous equations which must be solved to obtain the desired answer.

Sample Problem #5

 A box of mass 10 kg rests on a horizontal floor.  The coefficient of sliding friction between the box and the floor is 0.25.  A boy pushes the box across the floor at a constant speed.  The force is applied downward to the box at an angle of 30º with the horizontal.  Calculate the force required.

Sample Solution #5

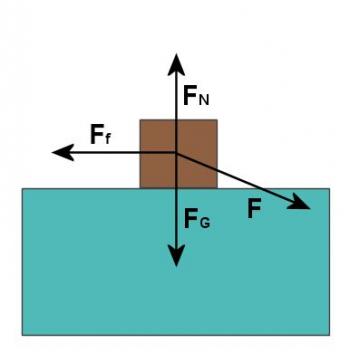
^{Figure 3.4.7}

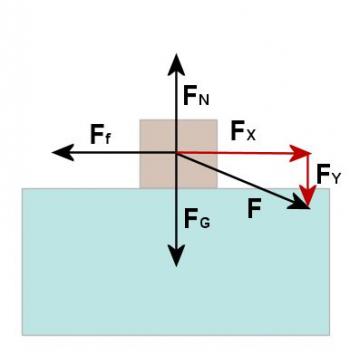
^{Figure 3.4.8}

The force of friction is  μ  times the normal force.  A common error at this point is to set the normal force equal to the weight but this is incorrect.  From Figure 3.4.8 it should be obvious that the normal force must be equal to the sum of the weight and the downward component of the applied force.  Thus we have:

but:

Therefore:

The student can demonstrate that the solution to this set of equations is:

This problem has many alternate forms and  the student should attempt to formulate some of these and solve them or at least be sure that he can draw the proper diagrams.  These forms include: The same problem with the force applied horizontally, the same problem with the box being pulled by a rope which makes a certain angle with the horizontal, the same problem with the box on a slope and a force applied parallel to the slope or at some other angle with respect to the slope.

Sample Problem #6

A light rope 10 m long is attached at each end to trees 8m apart at points the same height above the ground.  An object having a mass of 50kg is suspended from the rope at a point 4m from one end as shown in figure 3.4.9.  Calculate the force in the rope on either side of the object.

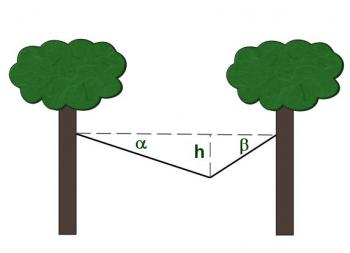
^{Figure 3.4.9}

Sample Solution #6

First it is necessary to determine the angle made with both sections of the rope with the horiz­ontal.  Since the rope is attached to the trees at the same height, the distance from the point of attachment to the lowest point is the same on each end.  It is labeled H on the dia­gram.  By applica­tion of the Pythagorean theorem to each of the two triangles we find that:

Solving these equations we find that:

Use trigonometry to find the values of the two angles, α and ß as follows:

sin(α) = =     therefore  α = 28.9º
sin(ß) = =     therefore  ß = 46.5º

Now draw a vector diagram as fol­lows where A and B are the unknown forces.

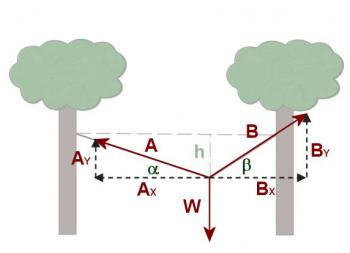
^{Figure 3.4.10}
 
Find the components of vectors A and B as follows:

Since the object is in equi­librium both x‑com­ponents and y‑comp­onents are balanced.  Therefore

Combining all of these equations and recall­ing that W = Ma_g = 490 N, we ob­tain:

Solve these to obtain:

The following diagrams are used for the practice problems below.

^{Figure 3.4.11}

^{Figure 3.4.12}

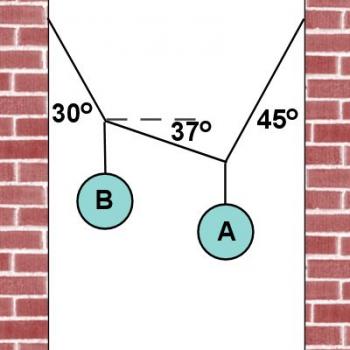
^{Figure 3.4.13}

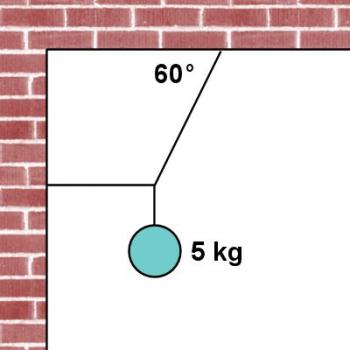
^{Figure 3.4.14}

^{Figure 3.4.15}

1.

A river is 3.0mi wide and flows 4.0mi/hr. A man can row 5.0mi/hr in still water. How long will it take him to row three miles down river and back? How long will it take him to row straight across the river and back?

2.

A pilot with a plane having a cruising speed of 200mi/hr wishes to fly to another airport 100mi to the north and return. A steady wind of 50mi/hr is blowing from the south. What is his total flying time in minutes for the round trip?

3.

A river flows due north with a speed of 3.0 mi/hr. A man rows a boat across the river; his velocity relative to the water is 4.0mi/hr, due east. What is his velocity relative to the earth?

4.

In the previous problem, how much time is required to cross the river if it is 2 miles wide? How far north of his starting point will he reach the opposite bank?

5.

A boy can throw a baseball horizontally with a speed of 20 m/sec. If he is in a convertible that is moving at 30 m/sec toward the North and throws the ball in a direction perpendicular to the direction in which the car is moving, what will be the actual speed and direction of motion of the baseball?

6.

A 100N object is suspended from the ceiling of a room by two ropes A and B. Rope A makes an angle of 30.0º with the horizontal and rope B makes an angle of 60.0º with the horizontal. Compute the tension in each rope.

7.

A 200‑lb object is hung from the mid‑point of a horizontal wire 20.0ft long. The wire stretches until the middle part sags 1.50ft. How much did the wire stretch? What is the tension in the wire?

8.

A rope 17.0ft long has its ends attached to two points 13.0ft apart in the ceiling of a room. If the maximum tension which the rope can withstand is 200‑lb, what is the heaviest weight which can be suspended from a point 5.0 ft from one end of the rope?

9.

A 400N block rests on a 30º, frictionless, incline. What force parallel to the plane is required to hold it stationary?

10.

A 600N sphere rests in a V‑shaped trough whose sides form an angle of 60º with each other. What is the force exerted by the sphere on each side of the trough?

11.

The rope supporting a child's swing is 5m long. A child is swinging back and forth on the swing, going a maximum horizontal distance of 1.5m from the vertical line through the bar supporting the swing. At the end of the swing, the tension in the rope is 600N. What is the combined weight of the child and the swing?

12.

A 100N picture is supported by a wire from a single hook. The ends of the wire are attached to the picture frame by two screw eyes 50cm apart. The length of the wire between the hooks is 55cm. Calculate the tension in the wire.

13.

Find the acceleration of the two blocks in Figure 3.4.11, where M₁ = 64kg, M₂ = 96 kg and Θ=30º. What is the tension in the rope? Assume that there is no friction.

14.

Block A (4‑lb) rests on a smooth board inclined at 30º with respect to a level table top. A cord passes from A over a frictionless pulley to an 8.0‑lb block B hanging at the side of the table. Find the acceleration of the blocks when released.

15.

A block has been placed on an inclined plane and the slope of the incline changed until the block will slide down at a constant speed once started in motion. The coefficient of sliding friction between the block and the incline is (μ). Calculate the angle of incline in terms of the coefficient of friction and show that it is the same regardless of the mass of the block.

16.

A box with a mass of 50kg rests on a horizontal surface. The coefficient of friction between the box and the surface is 0.25. A man wishes to move the box across the floor but it is too heavy to carry. He can move the box by pushing on the box with his force applied at an angle of 30º above the horizontal or by pulling on a rope with the force again applied at an angle of 30º above the horizontal. Calculate the force required in each case.

17.

In the system pictured in Figure 3.4.12, a 34kg block slides along a smooth plane of height 7.0m and length 15m. The ball at the lower end has a mass of 29kg. The system is released when the lower ball is 3.5m above the ground. How fast is the lower ball moving when it reaches the ground?

18.

Two objects, A and B, are hung from a rope which is attached to its ends to vertical walls, as in figure 3.4.13. If object A weighs 140‑lb find the weight of object B.

19.

An acrobat whose weight is 150‑lb stands at the middle of a wire which is stretched between two hooks 20.0ft apart. What is the tension in the wire if the lowest point on the wire is 4.0in below the support?

20.

A body of mass 5.0kg is supported by cords as shown in Figure 3.4.14. Calculate the tension in each of the three sections of the cord.

21.

Two identical smooth cylinders, each weighing 400N, are placed lengthwise in a narrow rectangular box as shown in Figure 3.4.15. The radius of the cylinders is 20cm and the width of the box is 60cm. What force is exerted by the bottom of the box on the lower of the two cylinders? What is the force exerted by one machine on the other? What force is exerted on the wall of the box by each cylinder?