In math and science we often talk about significant figures, or significant digits. Significant figures are the digits of a number which actually are relevant in indicating how precise a number is. That may be a little difficult to understand, so let's take a look at a simple example.

Suppose I have a meter stick that is marked in centimeters (not millimeters), and I decide to use it to make some measurements. So I measure two objects. 

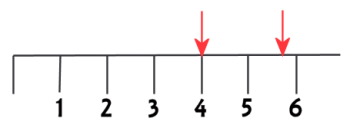
How long is the object measured at the first red arrow? It's 0.04 meters, right? What about the second object? Well, it's somewhere between 5 and 6 centimeters. I don't really want to say it's 6 centimeters, because it's obviously not quite 6. So I make an estimate, and I say it's 5.7 centimeters, or 0.057 meters. It's generally considered acceptable to estimate to the nearest tenth of whatever your smallest unit on your measuring device is. If the units are something as small as millimeters, you might not be confident enough of your estimating skills (or your eyesight!) to estimate to a tenth of a unit. If that's the case, you should estimate to the nearest fifth (0.0, 0.2, 0.4, 0.6, 0.8) or to the nearest half (0.0 or 0.5). 

Now I'd like you to consider the following: would it make sense to refer to that second measurement as 0.05724931 meters?

It absolutely would not! Having all those digits after the decimal place suggests I have made a very very very precise measurement. In fact, people would conclude that I have a meter stick that has markings down to the micrometer! 

This is not a good thing. It's almost like lying; as a scientist you've claimed to have something better than you really do. You're like the fisherman who caught a 6 inch fish, but claims it was two feet long! If you didn't measure to the nearest micrometer, you better not have an answer that has that many decimal places.

Why is it so bad to have extra decimal places? For one thing, extra decimal places can very easily convert into lost money, or project delays. That's no joke. Suppose you needed to have a machine shop build replacement parts for your part that's 0.057 meters long. They'll set up their equipment and build it, no problem. But suppose you give them the length as 0.05724931 meters. What happens then? Well, now they have to measure everything to the nearest micrometer instead of to the nearest millimeter, and the extra work that goes into doing that makes your product more expensive, but not a bit better (and they might even refuse the job, saying they don't have the right equipment to do that!).

On the other hand, it wouldn't make sense for us to use less than three decimal places, would it? If we called it 0.06 meters, we'd lose some of our precision. (Imagine that same machine shop building replacement parts that were 3 millimeters too long, just because you got lazy and dropped off a digit!) So when we write 0.057, we're not just stating the length of the object; just by writing those digits, we're declaring how precise our measurement is.

And this, by the way,is reason for estimating to the tenth, fifth, or half; 10, 5, and 2 are all factors of 10, so estimating to one of these will only introduce one extra digit into your answer. If, for example you estimated to the nearest fourth, you would have 0.0575, which suggests that you are precise to a hundredth of a centimeter instead of to a tenth of a centimeter.

But here's something interesting...if we're claiming that we measured the 0.057 to the tenth of a centimeter, didn't we measure the 0.04 to the same precision?  We sure did!  And we know we did, because we used exactly the same measuring tool to do the measuring. And yet, at a glance, it looks like 0.057 was measured more precisely, because it has an extra digit after the decimal place. So we agree that in a case like this, we're not going to write our first measurement as 0.04; we're going to write it as 0.040. That zero at the end doesn't change the value, does it? The reason it's there is to let people who see our numbers know that we've measured that value as precisely as we measured the 0.057.

We're always encouraged to be as precise as possible, and we understand that more decimal places indicates a more precise answer, so it may seem counter-intuitive to round an answer to get rid of decimals. But the issue is that we need to be as precise as possible, but not appear more precise than we really are.

Consider this example. Let's suppose that our 4.0 centimeter (0.040 meter) object we measured earlier needs to be cut into 3 equal length pieces. Since we've measured the object at 0.040 meters long, we divide that by three to find out how long each piece will be: 0.013333...

Look at that answer! How many decimals does it have? An infinite number, right? It never stops. But do we really know the answer with that kind of precision? Of course we don't! Because we don't have that kind of precision on the number we started with (0.040). Since we don't have infinitesimal precision in our measurement, we can't have infinitesimal precision in our answer. Therefore, we must have rules for rounding our answer in order to guarantee that we have the proper level of precision in our answer - in order to guarantee that we don't have too many or too few place values. This is why we need to have significant figures rules.

Hopefully this little explanation will help you understand why significant figures (sometimes called "sig figs") are important. There are a lot of rules to using significant figures, and we'll get into some of those in the next section.

1.

I measured an object that is 0.721 meters long, but I used a meter stick that is only marked to the nearest decimeter. What would my measured value be?

2.

City A is 125.825 miles from City B. I measured the distance between them by using the mile markers on the highway. How would I write my measured value?