Life beyond Vortex Based Math
If we set aside the fact that "Vortex Based Math" isn't actually math at all, but rather, cute parlor tricks for middle school students, and Baha'i mysticism (when you see the acronymVBM, you should think "Vortex Based Mysticism"), we can still get some pretty pictures (and maybe ask some real mathematical questions) by expanding the concept to base N. Here's what Marko-10 might have come up with if he wasn't still counting on his fingers after all these years. By the time you finish this page, you will discover that not only is Marko-10 wasting his time on one out of an infinite number of "vortex" systems, but that eachof those infinite "vortices" has an infinite number of related systems!
You'll note that our Vortex-10 diagram doesn't look like Marko-10's diagram. His diagram isn't even a proper mapping, since instead of 3 and 6 mapping to each other, he mapped them both to 9 (purely an aesthetic choice on his part, but mathematically inappropriate). We opted not to cheat, and do our diagrams as proper mappings.
RED: Red lines represent loops - numbers that form a continuous cycle, with the last number in the loop mapping into the first one. The more loops there are, the darker the shade of red used.
GREEN: Green lines are what I call "feeders." They either feed directly into a loop, or they feed into the "magic number."
Every time you view a vortex, you'll see at the bottom of the display a count of loops and feeders. If the number of feeders is zero, and the number of loops is one, this means that every number in the circle (except the "magic number") form one great big loop. See Our Babyblonian Vortex as an example.
Use the arrows to scroll through bases, type a base number, or just hit auto and let it run for awhile to see what happens. Enjoy!
Further Exploration
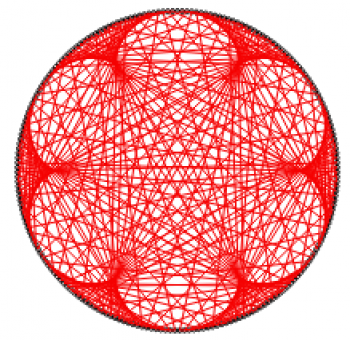
In all of this, even though we've generalized to base N, we've still severely limited our approach, so here's the next step for anyone who wants to explore this futher... What happens if we do tripling or quadrupling instead of doublingto create our mappings?
I'll give you two little tidbits to tantalize your curiosity.
- The image here is Vortex-212-7 (base 212, with a septupling operation) One loop, no feeders.
- Call Marko-10's diagram Vortex-10-2, because it's in base ten, with a doubling factor. Would you be surprised to hear that Vortex-10-5 looks identical to it? Except...the loop runs counter-clockwise instead of clockwise! Can you figure out the mathematics of why that happens? It may be more obvious than you think! (And no, for all the mystics, this doesn't make Marko-10's diagram "special" - similar behaviors can be found in all non-prime bases...whoops! I just gave a hint!)
You can change the multiplier from two to other values by selecting a value in the multiplier form.
Interesting Observations and Questions
Can you work out proofs for these observations? Some of them I have taken the time to prove, some I have not, so it's possible that they're not all true. Unless a k-value is specified, each of these statements assumes a doubling factor (k = 2).
- In every Vortex-N, N - 1 maps to itself.
- If N = 2x + 1, there are no loops (Vortex-9, Vortex-257).
- If N = 3x + 1, there is a loop of length 2 (Vortex-10, Vortex-25).
- If there is a loop of length 2, it is always represented by a horizontal line (note that this is not necessarily true for multipliers other than 2: Vortex-16-4!).
- All Vortex-N diagrams are symmetrical across the y-axis.
- If N = 2x, there are no feeders, if N = 2x + 1, there are feeders.
- If N = hx + 1, Vortex-(h+1) is embedded in Vortex-N. (for h = 11, Vortex-12, Vortex-23, Vortex-45)
- If N = k, each digit of Vortex-N-k has the "magic number" behavior.
- If N = kx + 1, there are no loops in Vortex-N-k (Vortex-10-3, Vortex-65-4).
Have fun exploring!
Professor Puzzler
Click here to read more about why the Vortex Based Mumbo-Jumbo movement isn't worth your time...




