Many students struggle with taking multiple inequalities and solving them to produce a set notation description of the solutions. This lesson outlines some examples to work through with students, and is followed by a worksheet for students to try as practice.

Why do we have students write solutions in interval notation? Because it's one of the best ways to ensure that students really understand how to combine inequalities. If they can correctly rewrite their solutions in interval notation, they understand what they're doing. 

We start from the most basic, and work our way through a variety of examples, growing more and more complex. Note that in this lesson this is done entirely separate from any work with absolute value inequalities; although absolute value problems are what produce many of the more complex examples, some texts don't take the time to well develop this capability before diving into absolute values.

Example One
Write the solutions of x > 3 in interval notation.

Solution One
If we were going to graph the solutions on a number line, we would put a circle around the point 3, but not fill it in (since 3 is not included), and then, since we are including values greater than 3, we would fill in the line to the right of the number 3, and then fill in the arrow on the right.

To write this in interval notation, we would write x ∈ (3, ∞). The round parenthis (either left or right) is referred to as an open endpoint, with "open" corresponding to an open (unfilled) circle. In other words, since we're not including the number 3, we will use an open endpoint. Someone will invariably ask, "Why is infinity open?" The answer to that question is that infinity isn't actually a number - it is a symbol used to represent something that has no end. And since it has no end, we can't exactly include an endpoint, can we?

If both endpoints are open, we refer to this as an "open interval."

Example Two
Write the solutions of x ≤ -1 in interval notation

Solution Two
For this, the interval notation is x ∈ (-∞, -1]. Students should readily understand the open endpoint at negative infinity; now we just point out that the square bracket is a closed enpoint. This means that the endpoint -1 is included in the solution set. If we graphed it on a number line, we would draw a circle around -1, and then fill it in.

This interval, which contains both an open endpoint and a closed endpoint, is referred to as a half-open interval.

Example Three
Write the solutions of 1 ≤ x ≤ 3 in interval notation

Solution Three
The solution to this is: x ∈ [1, 3].  Before we get there, however, I draw two number lines - one for 1 ≤ x, and one for x ≤ 3. I draw these two number lines one directly above the other. I also use two different colors for the two graphs.

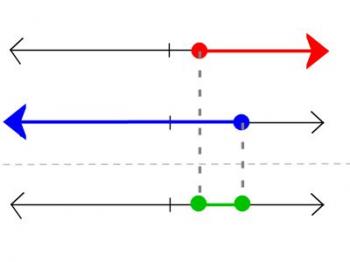
Notice that I've colored x ≥ 1 red, and x ≤ 3 in blue. I tell my students that there are two "points of interest." A point of interest is any point on any of those number lines that gets circled (regardless of whether or not the circle is filled in). A point of interest is a point where we change from included to not included (or vice-versa). A point of interest can also be a hole punched out of a set of solutions, or a single solution point. Essentially, a point of interest is a point at which something changes.

Then I show them that every point of interest in either of the top graphs need to be marked on the final graph. At first, we just circle them, because we're not thinking about whether or not they're included. We just know that they're important.

Since the notation 1 ≤ x ≤ 3 is a shorthand notation for "and" (1 ≤ x AND x ≤ 3), we're only going to include points if they are in the red graph AND the blue graph. So we start to the left of the red "point of interest" and ask, "Are these points included in both the red and blue graphs?" Since the answer is "No," we don't include these points. Then we ask, "What about the red 'point of interest'? Is it included? in both?" Yes, it is, so we fill in that dot on the resulting graph. Then we look at the section between the points of interest, then we look at the blue point of interest, and then the section to the right of the blue point. For each point and region we ask, "Is this included in both graphs?" If it is, it is also in the final solution.

Now that we have the graph visualized, it's easy to see that the solution is the interval [1, 3]. Since both endpoints are closed, we call this a closed interval.

Example Four
Write the solutions of x < 1 or x ≥ 3 in interval notation.

Solution Four

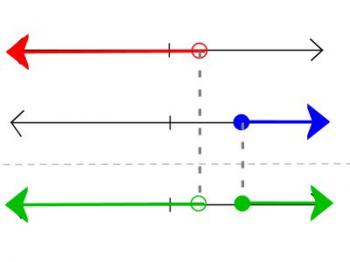
For this one we also do two graphs. This time they look like the diagram here. We begin the same way as before; since both 1 and 3 are points of interest in the top graphs, we circle them in the resulting graph. This time, we have an OR combination, so instead of looking for points that are in both graphs, we are looking for points that are in at least one of the graphs. We begin to the left of the red point. Since that's included in the red graph, we include it in the result. The red point is not included, so we don't include it in the result. And so forth, from left to right, we consider each region and point. 

When we're all done, we see that this time we have two regions. We can't write that with a single interval; we need two intervals. We write it like this: x ∈ (-∞, 1) OR x ∈ [3, ∞). We have a special way of writing "or" in set notation; it's the union symbol:  

x ∈ (-∞, 1) ∪  [3, ∞)

Example Five
Write the solutions of x ≠ 1 or x ≤ 3 in interval notation.

Solution Five

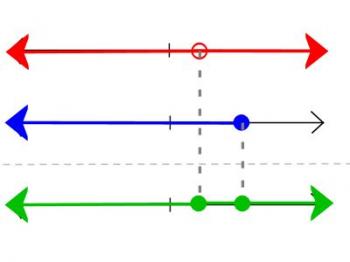
This one can be a little confusing for students, because we start with two points of interest, and when we're done, we have no points of interest. As before, we begin by graphing. The first graph is all the points on the number line except 1. As a test, ask your students to write that in interval notation: x x ∈ (-∞, 1) ∪  (1, ∞).

No we work through the same reasoning as we did for the previous problem, which was also an "OR" problem. When we are all finished, we have a graph that looks like the green one.

"Wait a minute," I say at this point, "Didn't I tell you that points of interest are points where the graph changes? But nothing changes at either of those green points. The green points are included, as is alll the stuff to the left and right of them! You know what that means? It means they're not points of interest any more. They're as boring as everything else on that number line! So we're not going to mark them with circles any more." Here I erase the circles, and fill in the gap with a line. Then I say, "It looks like we're including the entire number line...so what's the interval for that?" And the answer is, x ∈ (-∞, ∞).

Example Six
Write the solutions of (x ≥ 3 or x ≤ 1) and (-2 < x < 2) in interval notation.

Solution Six
This is the culimination of all the work we've done up to this point. Here we have two parenthetical inequalities, one of which is an OR and the other an AND. The two inequalities are combined with an AND. When does something like this come up in mathematics? Students who are solving absolute value inequalities may be given a pair of inequalities which match these solution sets, and be asked to find all values that satisfy both inequalities.

In this case, we graph each of the parenthetical inequalities separately. The first one graphs to all the points to the left of 1, and to the right of 3, and including those two points of interest. The result, in interval notation, is x ∈ (-∞, 1] ∪  [3, ∞).

Then we deal with the second set of inequalities, which contains all the points between -2 and 2, exclusive. In interval notation, that looks like this: x ∈ (-2, 2).

Now we take those two graphs and draw them on top of each other, and we combine them with "AND" which means a number is included in the solution if it is a solution in BOTH graphs. The resulting set is:

x ∈ (-2, -1]