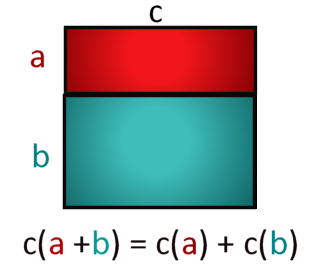Distributive Property Illustrated
Lesson Plans > Mathematics > AlgebraSlide Show
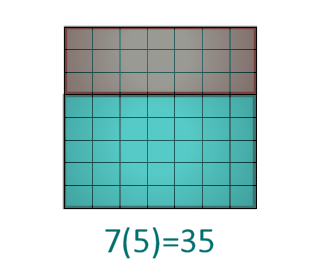
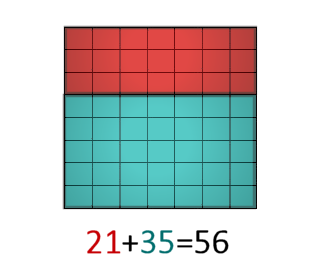
7(3 + 5) = 7(3) + 7(5) = 56
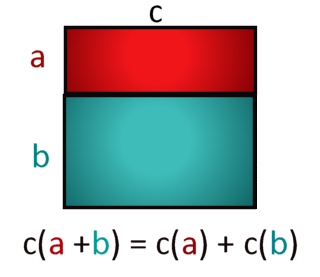
Lesson Plan/Article
Distributive Property Illustrated

When I'm teaching Algebra, and working on a problem on the board, when I say to my students, "What should we do next?" Nine times out of ten, the answer they give me is, "Use the distributive property!" And nine times out of ten they're correct. The distributive property is one of the most ubiquitous properties for algebraic manipulation; you simply can't get away from it.
But why does it work? Some students will simply accept your promise that it will always work, others will want to try a few examples to convince themselves that it works, but some will want a little more "demonstration". For those students, I like to give an illustrated, geometric picture of the property.
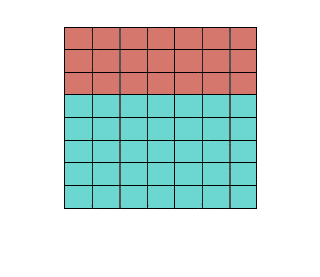
I begin with a rectangle that is eight units tall and seven units wide, split into two smaller rectangles, as shown below (and in the slide show).
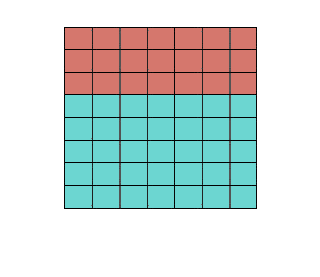
Now I point out that we can easily calculate the area by finding the height and the width, and multiplying them together. This is the second slide.
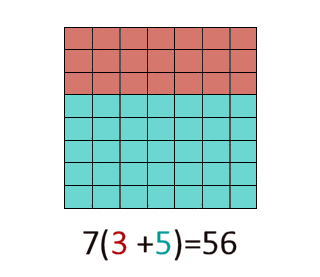
Then I ask, "Couldn't we also find the area by finding the areas of the two smaller rectangles, and then adding them together?" The answer to this question is, "Of course!"
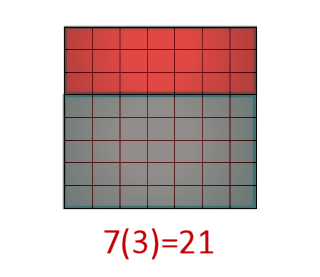
The next two slides show the same triangle, with the upper part highlighted, and then with the lower part highlighted, and the area calculations underneath.
Finally, we show that the sum of these is 56, the same as calculating the whole area at once.
As a follow-up, you may wish to generalize this to any a, b, and c. In this case, we dispense with the dividing cells in the rectangle, and label the two heights a and b, with the width labeled as c. This allows us to show that it always works, regardless of the values.