The slope of a curved line is one of the first things we must help students visualize in their path toward understanding what calculus is. It's easy to see what the slope of a straight line is, and students have studied this concept throughout their Algebra and Pre-Calculus classes. What makes the study of slopes different in calculus is that we're no longer limiting ourselves to straight lines.

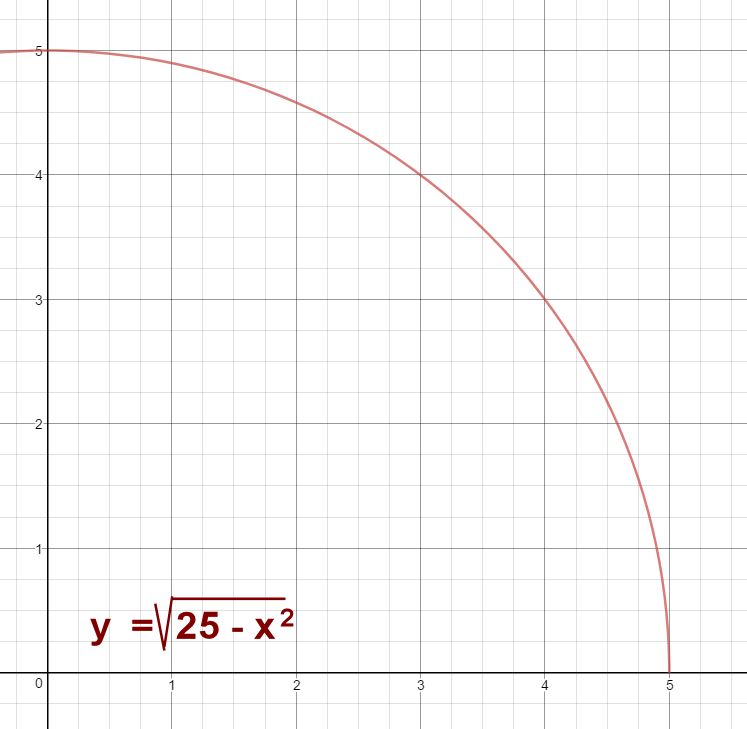
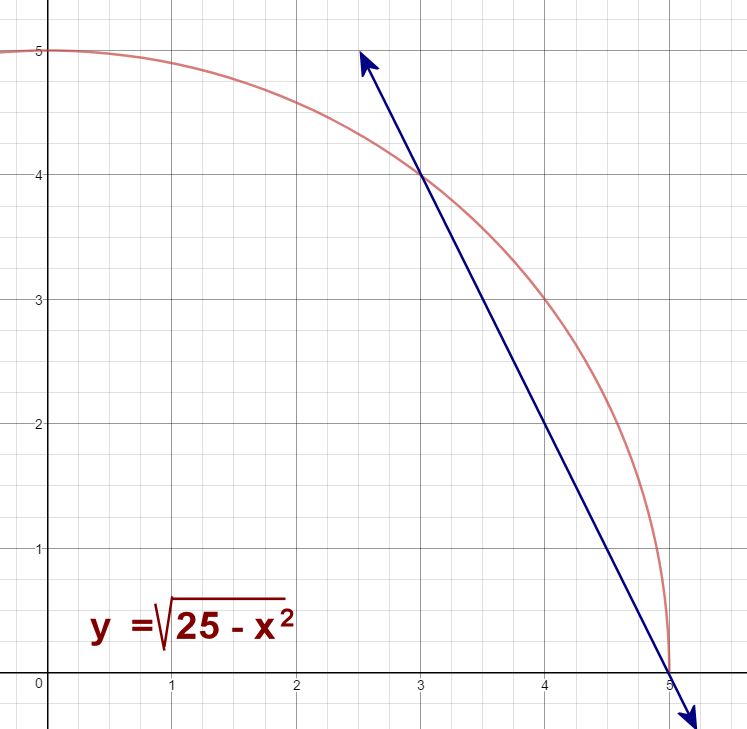
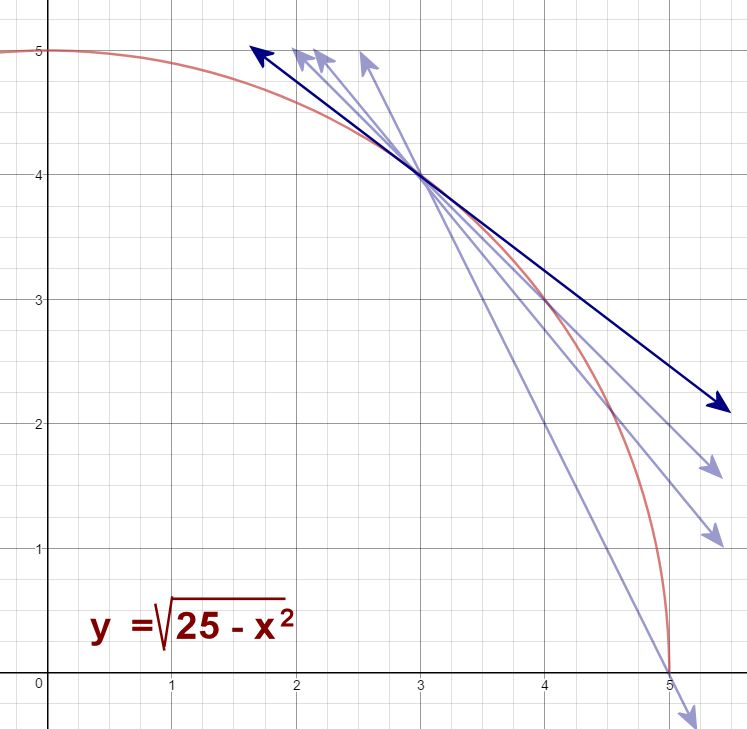
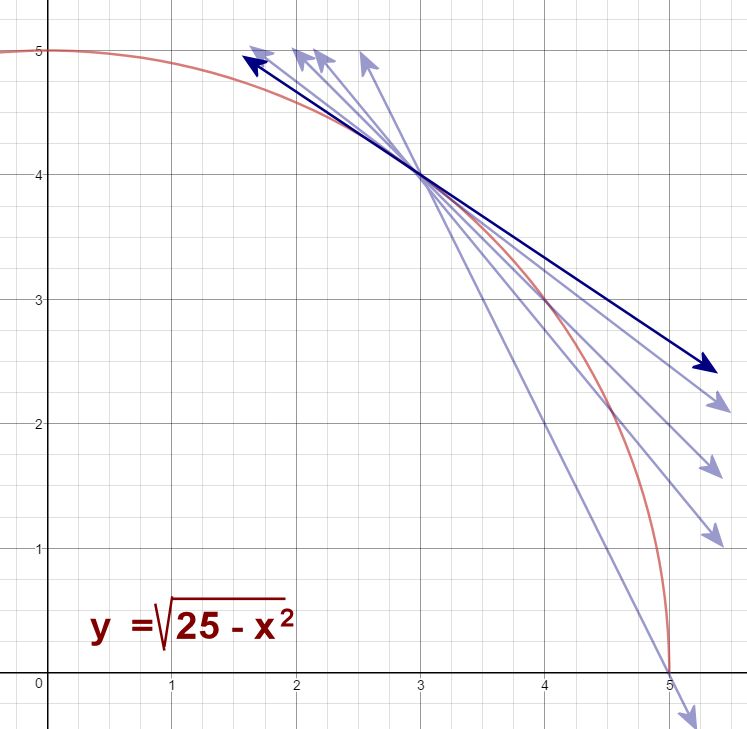
When talking to students about slopes of curved lines, my preference is to begin with a circle, such as x² + y² = 25. I've specifically chosen a circle because we can use approximation methods to zero in on the slope, but we can also use geometry concepts to identify the exact value, thus allowing us to verify our approximation. I've chosen this particular circle because a radius of 25 lets us focus on a Pythagorean Triplet (3, 4, 5), which gives us nicer numbers to work with. We're going to focus on the point (3, 4) in our example. If you used a circle like x² + y² = 169, you would probably want to focus on the point (5, 12).

Since we want to think in terms of functions, we're going to rearrange this equation to obtain y = . The first slide in our slide show is a graph of this.

We then raise the question, how could we approximate the slope of the tangent at the point (3, 4)? We show students that we could get a rough approximation by considering the secant that passes through (3, 4) and another point on the graph. For our first point we choose an easy one - the point (5, 0). The line containing both (3, 4) and (5, 0) is = = -2. This is illustrated in the second slide.

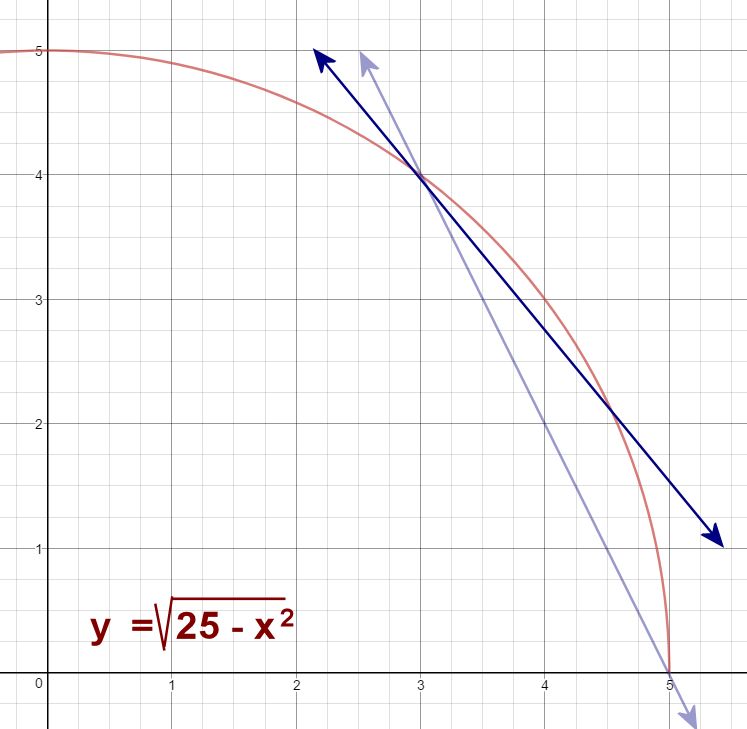
As we continue through the next few iterations, encourage students to keep their y-values in their calculators, rather than rounding them. In other words, they should calculate the coordinate for each secant, rather than using the rounded value we provide in the lesson plan. This will give more precision, and avoid the confusion of rounded answers that fluctuate up and down from one iteration to the next.

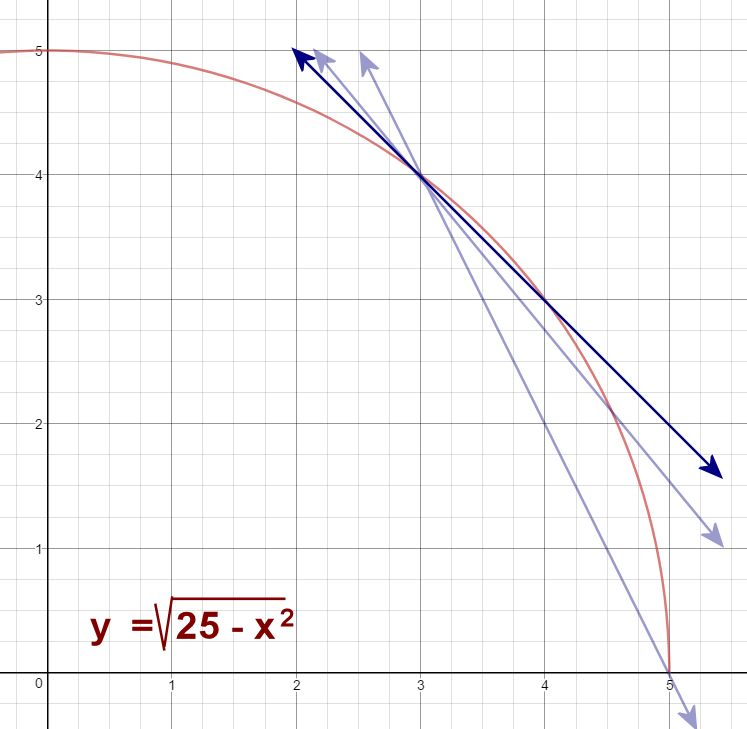
For our next iteration, we find the slope of the secant passing through (3, 4) and (4.5, 2.1794). This slope is = -1.2137. [Third slide]

Then we find the slope of the secant passing through (3, 4) and (4, 3). This slope is another easy one: = -1. [Fourth slide]

Then we find the slope of the secant passing through (3, 4} and (3,5, 3.5707). This is = -0.8586. [Fifth slide]

For our next iteration, we consider (3, 4) and (3.1, 3.9230). This is = -0.7699. [Sixth slide]

At this point we compare all of these values: -2, -1.2137, -1, -0.8586, - 0.7699, and we note that while the slopes are increasing (heading toward zero), the increase is getting smaller and smaller for each iteration. Are we homing in on the actual slope? Although we don't have another slide for it, have the students try (3, 4) and (3.01, 3.9925). The slope is = -0.7520.

If you want the students to try one more, do (3, 4) and (3.001, 3.9992). The slope is = -0.7502.

It appears, from all of this, that the slope of the curve at the point (3, 4) is about -0.75. It would be nice to have a way to verify that this method of approximating the slope really is legitimate. And here we come to the reason we started with a circle; if your equation is a circle, you do have a method of verifying! [Seventh slide]

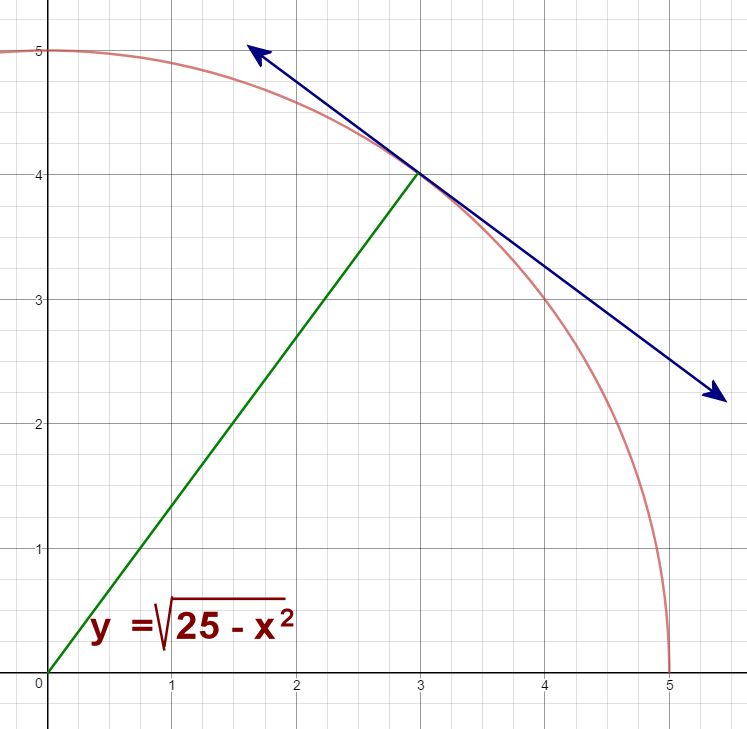
In this slide, we have a radius drawn from the center of the circle to the point (3, 4). Can we calculate the slope of this line segment? Of course we can! It's easy! = . But how does a tangent to a circle relate to the radius to the tangency point? They're perpendicular, right? So the slope of the tangent is the negative reciprocal, or - = -0.75.

This demonstration helps students visualize that our method of approximating the slope really does work.

From here, give the students a simple equation like y = 3x², and ask them to calculate the slope of the function at the point (2, 12). They will use the method of approximation to home in on a value of 12.

Example point: (2, 12) and (2.001, 12.012003): Slope = = 12.003.