One of the extraordinary results obtained in the study of calculus is the Fundamental Theorem of Calculus - that the function representing the area under a curve is the anti-derivative of the original function. Another way of saying that: If A(x) is the area underneath the function f(x), then A'(x) = f(x). This lesson provides a rough geometric proof of the FTC. We'll do a little bit of "hand-waving" along the way, since this lesson was designed for students getting an overview of what calculus is all about, rather than for students who are doing an in-depth study. In other words, this is a good lesson for students who won't be taking calculus until next school year, but you want to give them a "taste" of it now.

First, I begin by reviewing with my students the following equation:

f'(x) =

I leave this formula on the corner of the board, because we're going to refer to it later. In fact, that equation, the limit expression of a derivative, becomes the big "Aha!" later on in the class.

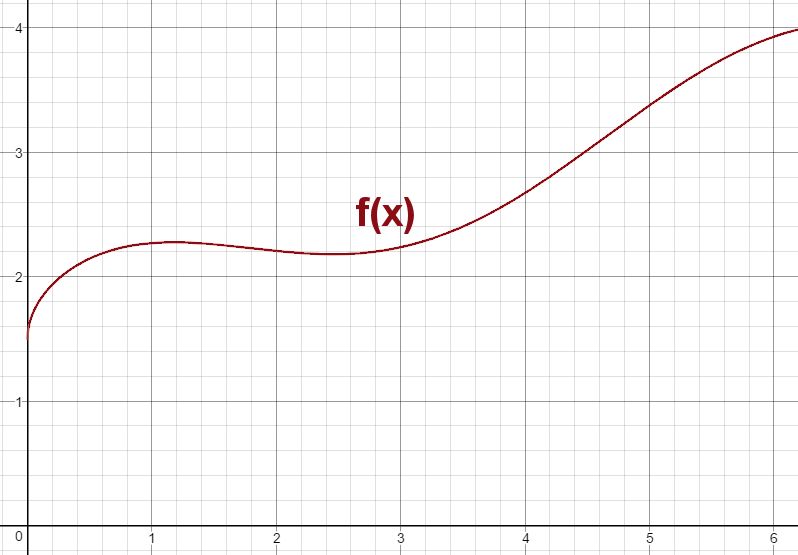
After reviewing the f'(x) equation, the first slide goes on the screen. This is just some "generic" continuous function f(x). The actual function I used was f(x) = + + 1, but that is irrelevant; we will never make use of that information in class.

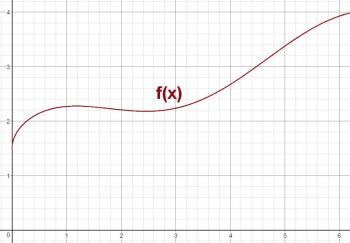
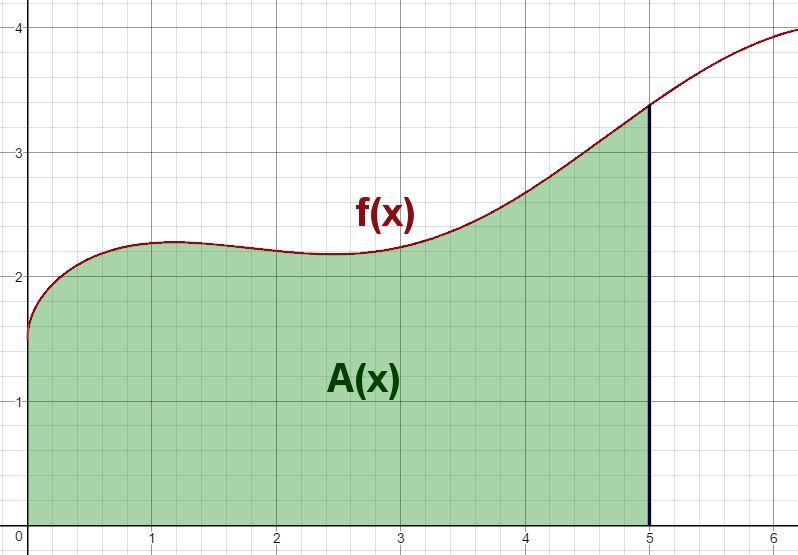
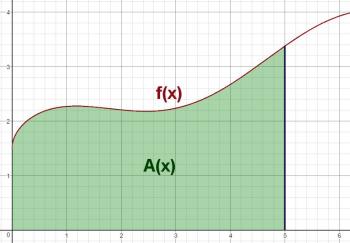
Now I point out that there is another function that is related to this function - I'll call it A(x), and it is the area underneath the curve. The second slide illustrates this function, showing the region we're interested in, marked in green.

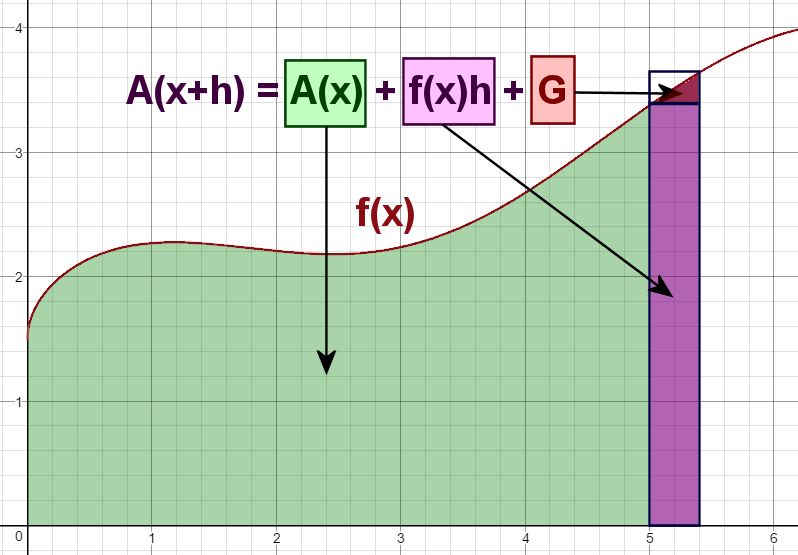
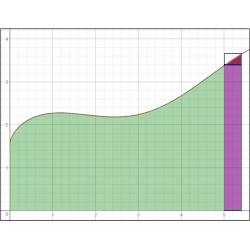
I point out to the students that it would be nice if we could determine some sort of mathematical relationship between f(x) and A(x). I wonder (out loud) what would happen if we did the same sort of (x + h) idea for areas that we did for slopes. In other words, what if we tried to find the value of A(x + h)? This is shown in the third slide:

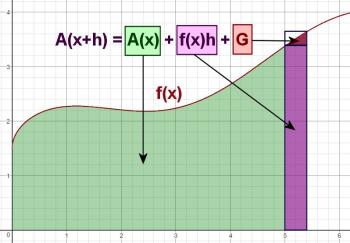
While this slide is on screen, I explain to them each of the colored regions:

• The green region is just A(x), which we established in the previous slide.
• The purple region is a rectangle. Its width is h, and its height is f(x); therefore, its area is f(x)h.
• The red region has unknown area, so I just labeled it G*.

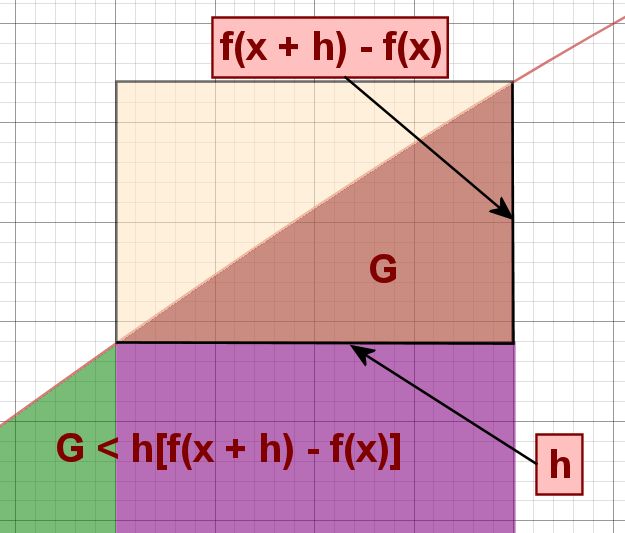
Even though we can't find the value of G, we recognize that it's less than the area of the tiny rectangle it fits inside. That area is h[f(x + h) - f(x))], because the rectangle's width is h, and its height is the difference between the function values at (x + h) and x. The next slide shows this by zooming in on G.

 

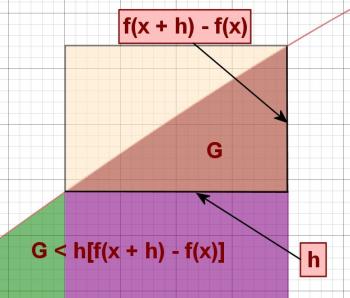
I'll write this inequality on the board (along with the f'(x) equation), and then we return to the previous slide. Now I ask my students to take the equation for A(x + h) and solve it for f(x). The result is:

f(x) = -

As h approaches zero, this becomes:

f(x) = -

We recognize that since G is less than h[f(x + h) - f(x)], then is less than f(x + h) - f(x), which approaches 0 as h approaches zero. Thus,

f(x) = , which gives us our "Aha!" moment:

f(x) = A'(x)

The area is the antiderivative of the function!

* If you wonder why I labeled the red region G, it's because it makes me think of a "gore." When regions of land are divided into rectangular plots, since the earth is curved, there will always be "leftover" chunks of land that are roughly triangular in shape that fit into the cracks between the rectangles. One of these leftover chunks is called a gore.