Print

When I took Calculus, both in high school, and then in college, they never taught me the "Two Cops and a Drunk Theorem." I've decided that my calculus students will never miss out on this wonderful theorem; it's one of the highlights of the class. Here it is:

Two Policemen and a Drunk Theorem

If two police officers are escorting a drunk man, it doesn't matter how much he wobbles back and forth between them, or what path they take, if they are able to keep him between them, and both cops go to the same jail cell, the drunk man will also go to that same cell.

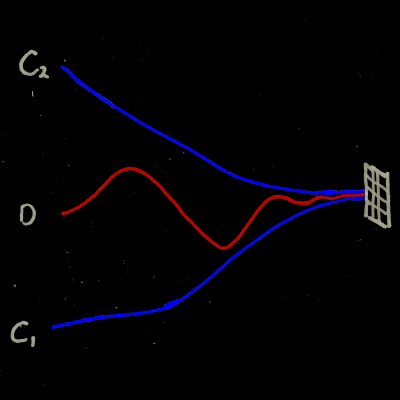
It's pretty silly, and doesn't seem very mathematical. But it's a very important theorem in calculus. Here's a visual of the theorem:

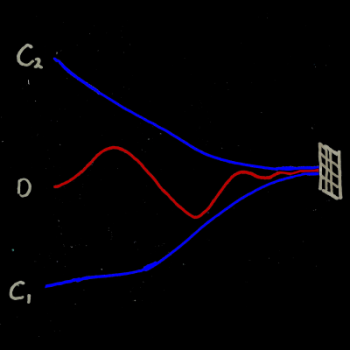
It makes sense, doesn't it? If the drunk can't disappear or teleport away, and the cops keep him always between them, and they both head for the same place, the drunk man has to end up in the same place. They don't even have to be "touching" him - they can be like sheepdogs herding the sheep. As long as the man stays between them, he ends up at the cell.

What is this "theorem," really? Even if you weren't already familiar with it, if you teach calculus, you can probably deduce where this is going - it's a cute illustration of the Squeeze Theorem or the Pinching Theorem. 

Let C₁(x) and C₂(x) be the "squeezing" or "pinching" functions, and D(x) be the squeezed function.

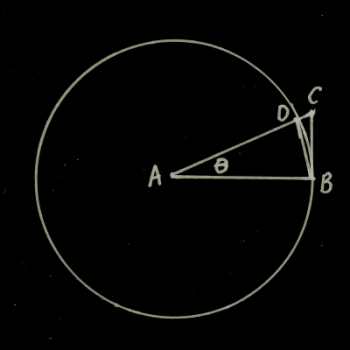
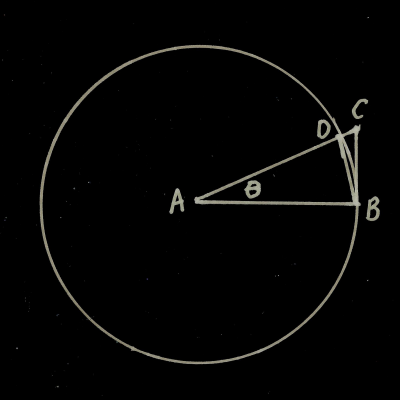
If, for all values of x in a neighborhood of c_x (the abscissa of the cell), C₁(x) ≤ D(x) ≤ C₂(x), and  =  = c_y (the ordinate of the cell), then  also equals c_y.

This is a really fun way of introducing the squeeze theorem, and almost certainly the most memorable way of doing so. Once the theorem is introduced, rather than developing a proof of it, I took my class through an example of how the Two Cops and a Drunk theorem can be used to prove that

lim

sin Θ

Θ

Θ→0

= 1.

We begin by drawing a unit circle (click the image for a larger view), with an angle Θ. In this circle, A is the center, B and D are the intersection points of the angle with the unit circle. I also extend AD to C, such that ABC is a right angle. This diagram has three interesting shapes in it: an isosceles triangle (ABD), a sector, and a right triangle (ABC). The isosceles triangle is fully contained within the sector, and the sector is fully contained within the right triangle, which means, if their area functions are I(Θ), S(Θ) and R(Θ), then I(Θ) ≤ S(Θ) ≤ R(Θ). (I used I, S, and R to indicate "isosceles", "sector", and "right").

But what are these functions? Well, the area of the isosceles triangle can be found using the formula A = absinC:

I(Θ) = sin Θ

The area of the sector is found using A = r²Θ (with theta in radians):

S(Θ) = Θ

Finally, CB = tan Θ, and since the area of a triangle is bh:

R(Θ) = tan Θ.

Thus, sin Θ ≤ Θ ≤ tan Θ.

Multiply the entire inequality by 2, and divide it by sin Θ:

1 ≤ ≤ .

Now, if we take the reciprocals (and flop the direction of the inequalities) we obtain:

1 ≥  ≥ cos Θ

This is a big deal, because we now have D(Θ) = sqeezed between the functions C₁(Θ) = 1 and C₂(Θ) = cos Θ. D(Θ) = is our drunk-man function squeezed between the two cop functions. So let's find the limits of the cop functions:

= = 1
  = = 1

Since both cop functions go to the same limit, and the drunk function is squeezed between them, our theorem tells us that  = 1

This is a beautiful result; it takes some basic geometric and trigonometric ideas and combines them with the cop-drunk theorem to create a useful limit.

It's good to point out that the cop functions led the drunk function to the cell, but the drunk doesn't actually enter the cell - at 0, the drunk function is undefined, because it involves a division by zero. Just like you can lead a horse to water, but you can't make him drink, you can lead a drunk function to the cell, but you can't make him enter.

Lesson by Mr. Twitchell