Many of my students really struggle with fractions. Specifically, they have a hard time remembering which process you use for which operation. Do you find a least common denominator when you're multiplying? Do you add across the numerators and denominators when adding fractions? Which fraction do you flip when dividing?

One of the most common mistakes I see (and I most often see it at the beginning of the school year when the students have had a whole summer to forget what they've learned) is this:

+ =

You see what they did, right? The two numerators get added to make a new numerator, and the two denominators were added to make a new denominator. Sometimes I find that a humorous example will help them remember things, so I do the following exercise.

First I pick a student from the class, and have a dialogue similar to the following (you might need to set this up in advance, if you're concerned that you can't ad-lib responses that don't fit the direction you're going).

Me: "Joe, what's your favorite kind of pizza?"
Joe: "Pepperoni!"
Me: "My favorite is cheese. Do you like cheese pizza?"
Joe: "Sure!"
Me: "But you like pepperoni better."
Joe: "Yeah."
Me: "Me, I like pepperoni, but I like cheese better. Are you hungry?"
Joe: "You bet!"
Me: "Okay, how about we split the cost of two personal-sized pizzas. One cheese, and one pepperoni. I'll give you a couple slices of my cheese pizza, and you can give me some of your pepperoni pizza. If we split the cost evenly, you'll get the better end of the deal, since pepperoni costs more than cheese."
Joe: "Sounds good to me!"

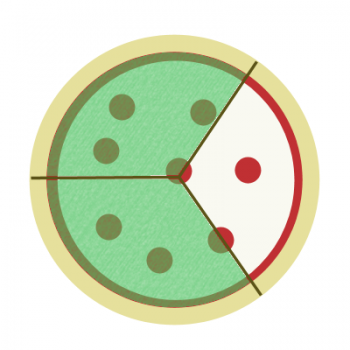
Now I go to the board, and draw a pizza. It's a pepperoni pizza, and it's cut into three large slices.

I say to Joe, "I guess, if you're going to get the majority of the pizza, you'll take two-thirds of it?"

If your students are anything like mine, and you haven't planned this out in advance, Joe will probably have some smart-aleck response like "No way! I'm not giving up that much pepperoni pizza!"

If that happens, you just have to get creative and say something like, "I'm sorry, Joe, but I don't have a pizza cutter, so we can't split that piece up." Or, you can just step out of the dialogue and say, "Oh, come on Joe, you just gotta play along with me!" Whatever you have to do, get Joe to agree with the split of pizza.

The second pizza is the cheese one, and it's divided into sixths. "Well, Joe, if we're going to do this fairly, how much of the cheese pizza do I need to give you?"

Of course, the correct answer is, "two-sixths" because is equal to , so I'm giving him as much cheese as he's giving me pepperoni. So I say to him, "Okay, so I'm going to add up how much pizza you have. And I'm going to use the method you guys like using." I write on the board:

+ =

"Wait a minute, Joe! is less than half of one pizza! This is great! You paid for a whole pizza, and you're getting less than half of a pizza! I think I should go into a pizza business with you! We should make deals like this ALL the time!"

The humor of this situation is effective in making the point memorable. I make sure I go through the details of how we really add those fractions - and then I say to the whole class, "Any time I see you doing fraction addition the wrong way, I'm going to just say to you, 'Would you like to split a pizza with me?'" 

The students all laugh, but they get the point. And we've turned a frustrating math concept into something they can laugh about, instead of freaking out over.