Trisecting an Angle with a Tomahawk
Lesson Plans > Mathematics > Geometry > ConstructionTrisecting an Angle with a Tomahawk

I have used the following activity as a research assignment for individual geometry students. I suspect it could be used equally well as a classroom activity. If you try it, please post your experiences in the forum!
It is an often stated premise that it is impossible to trisect an angle. This is a vague (and inaccurate) restatement of a mathematical truth. First, it should be noted that the key phrase "with a straight-edge and compass" is missing from the statement. Second, some angles (such as a ninety degree angle) can be trisected with a straight-edge and compass.
Instead, we should say it is impossible to devise a construction method of trisecting any angle with a straight-edge and compass. This lesson helps prove the point by demonstrating that angles can be trisected using a unique tool called a 'tomahawk', that any student can build.
The Tomahawk is actually going to be created on paper, and then cut out with scissors, so get ready to be 'crafty'. First, draw a straight line of arbitrary length (my line is about three inches long), and trisect it.
Question: Can you trisect a line using just a straightedge and compass? Since the line is of arbitrary length, you don't really need to worry about that; just make the line longer than you need it, and mark off three equal length segments on it.
Now, using one of your trisection points as the center, and the trisection length as the radius, draw a semi-circle on one side of the line. Your figure should now look like this:
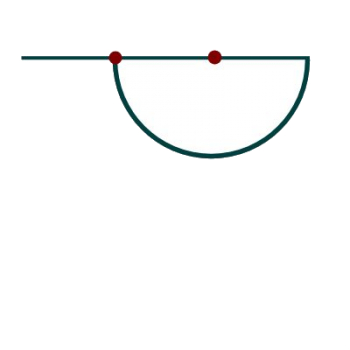
Now construct a perpendicular to the original line, passing through the trisection point which is on the circle. The length of this line is also arbitrary; use the four to five inch range.
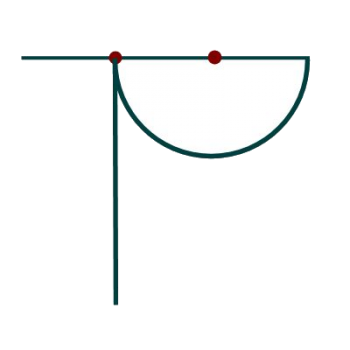
That's all the construction needed, and you're almost ready to cut out your tomahawk. Of course, it's going to be tough to "cut out" those lines sticking out of the semi-circle, so let's add a couple extra lines in. It's wise to make the "extra" lines curved, so you don't get confused about which line is the "real" line, and which one you added in. In the diagram below I added the extra lines in red. Now you can cut out around the outline of the tomahawk.

Now you're ready to trisect an angle! Everything up to this point was easy; this part can be a little tricky, because you have to put the tomahawk in exactly the correct position. The tomahawk has to touch the angle in exactly three places:
- The vertex of the angle has to touch the straight edge of the tomahawk 'handle'
- One ray of the angle has to touch the 'sharp' tip of the tomahawk
- The other ray of the angle has to be tangent to the semi-circle
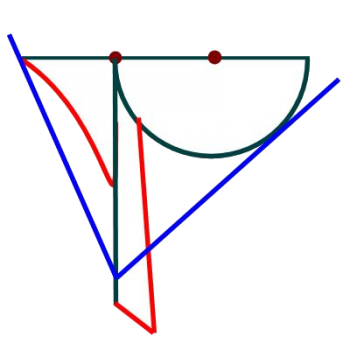
With the tomahawk in this position, the angle is trisected by the "handle", and by the line (not shown) connecting the angle vertex to the center of the semi-circle. A geometric proof of why the angle is trisected is within the reach of high school geometry students, and makes a great conclusion to the project.

