Students often struggle with the concepts of union and intersection of sets. The trouble is typically remembering which is the combination of both, and which is only the parts they have in common. 

In order to help students with this, I have two images I like to show them. One image goes with each of the concepts.

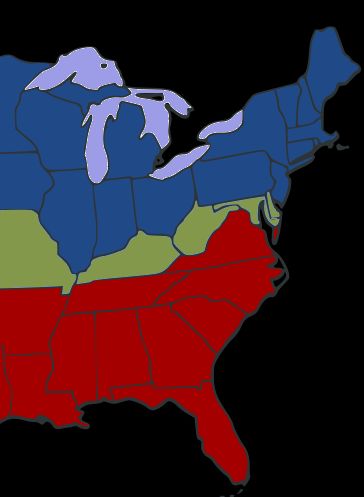
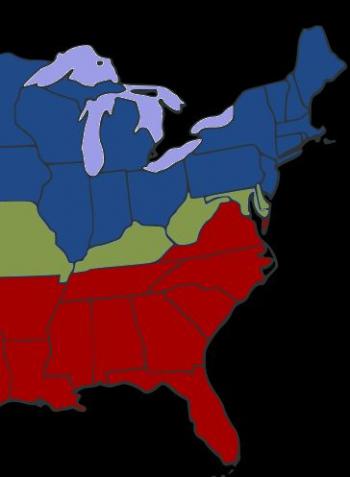
The first image shows the breakdown of the states during the civil war. The blue states are the northern Union states. The red are the southern Confederacy. The states in the middle are known as the "border states" - slave states that didn't seccede. I'll ask my students, "Why were the northern states called 'The Union'?" A good answer to this question points out that the U.S. Consitution refers to states forming a "more perfect union" - the idea is, all the states together.

This is a nice picture, because we can picture the states as elements of sets - north, border, and south. When the Civil War was over, the United States was (as it had been before) the union of all the blue, green, and red states. So when students are struggling to remember what "union" means, I tell them to picture the map, and the fact that the UNION was all the sets combined.

The other picture is of a roadway intersection. I ask the students, "where is the intersection?" They tell me it's the part in the middle. I say, "Wait a minute! It isn't the whole road?" No, the parts away from the center aren't part of the intersection.  "So the cars that are in the intersection..." I say, and they reply, "...are the ones in the middle."

I encourage my students to think of the cars as being elements of a set - the set of cars on one road, and the set of cars on the other road. This is helpful, because then when they're trying to remember what to include in the "intersection" I just say, "Which cars were on the intersection?" And that helps them remember.

When it comes to remembering the symbols, of course, ∪ looks like a "U", which will help students remember it is the symbol for "union." The worksheet below allows students to practice union and intersection concepts.