Arithmetic Angles
Pro Problems > Math > Geometry > TrianglesArithmetic Angles
The angles of a triangle are in arithmetic progression, and the difference between the largest and smallest angle is 42 degrees. What are the three angles?
Solution
In order to make it feasible for teachers to use these problems in their classwork, no solutions are publicly visible, so students cannot simply look up the answers. If you would like to view the solutions to these problems, you must have a Virtual Classroom subscription.Similar Problems
Triangle and Rectangle
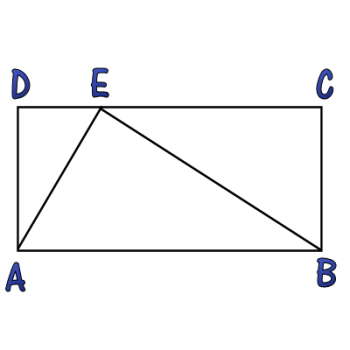
In the diagram displayed, the triangle splits the rectangle into three similar triangles. Find the value of AD2 divided by the product of DE and EC.
Three Two-Digit Angle Measures
The measures of the angles in a triangle are all two digit numbers, and two of them end in 3. Exactly two of them contain the digit 4. None of the angle measures are multiples of three. What are the measures of the angles?
Angle Measure
Line segment AB is intersected by segment DC, with D on AB, between A and B.
In triangle ADC, m∠ADC = 30º + x and m∠DAC = 50º
In triangle ABC, m∠ACB = 115º + x
In triangle CDB, m∠CDB = 140º + x
Find m∠CBD.
Quadratic Triangle
The angles in a triangle have measures x2 - 5, 2x + 18, and x + 37. What is the measure of the largest angle in the triangle?
Triangle in a Square
If the perimeter of the triangle (in linear units) is equal to the area of the triangle (in square units), what is the length of the side of the square?
Three Triangles
The angles in a triangle have measures x, x + 10, and y.
The angles in a second triangle have measures x + y, 40, and 50.
The angles in a third triangle have measures x – y, 40, and z.
What is the value of z?
Two Triangles with Angle Measures
In a triangle, the angles measures are: 3x + 44, x, and 2x - 20. In a second triangle, two of the angle measures are x + 20 and 2x - 5. What is the measure of the third angle?
Angle Bisector
In the diagram shown,
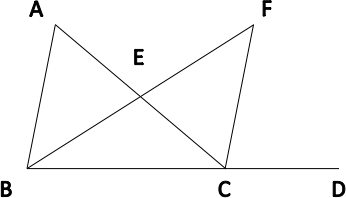
m ∠DCF = 80
m ∠ACF = 30
m ∠FBD = 50.
If segment BF bisects ∠ABD, find m ∠BAC.
Forty-five and Thirty
Two of the angles of a triangle are 45 degrees and 30 degrees. The altitude from the third angle has length 15 units. What is the triangle's area?
Split Triangle
Segment AD is drawn in triangle ABC, with D on side BC. Given the following information, determine the measure of angle ADB.
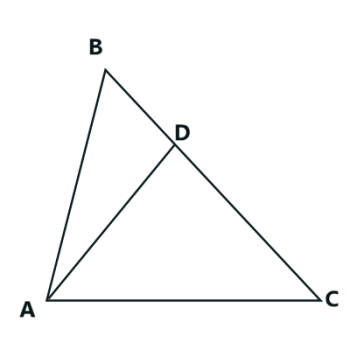
measure of angle BAD = x
measure of angle CAD = 2x
measure of angle ADC = 2y
measure of angle ABD = y
measure of angle ACD = x + y


