In the previous section we learned that two triangles are similar if they have three pairs of congruent angles. Actually, we learned that if they have twopairs of congruent angles, that's enough to know that the third pair has to be congruent.

In this section we'll learn about relationships between sides of similar triangles. Let's start with our triangles from last time:
 

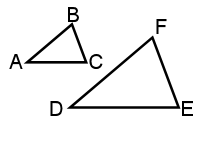
Suppose I told you that AB = 5 and DF = 10. You might think, "Oh, triangle DFE is twice as big as triangle ABC!" And you'd be right - in the sense that every side of the second triangle is twice the size of the corresponding triangle in the first triangle.

Thus, if I followed that up by saying that AC = 7, you should be able to conclude that DE = 14, because that's twice 7.

We say that the sides are proportional, which means that the ratio of corresponding sides is the same for each pair.

In other words:

AB / DF = AC / DE = BC / FE.

So if I told you that BC = 4, you could set up an equation:

AB / DF = BC / FE. Now plug in the values you know:

5 / 10 = 4 / FE

This is very easy to solve for FE - and the result is 8!

Example 1: ABC ~ WXY. If AB = 5, WX = 15, and BC = 3, what is the length of XY?

Solution: AB / WX = BC / XY. Plugging in values gives us: 5 / 15 = 3 / XY. Solving for XY gives us XY = 9.

Example 2: ABC ~ DEF. If AB = x, BC = x + 2, DE = x + 6 and EF = x + 11, what is the value of x?

Solution: x / (x + 6) = (x + 2) / (x + 11).

x² + 11x = x² + 8x + 12

3x = 12

x = 4

1.

ABC ~ XYZ. If AB is 10, XY is 5, and BC = 14, what is the length of YZ?

2.

DAB ~ TOW. If DA = 12, AB = 6, and TO = 8, what is the length of OW?

3.

ABC ~ DEF. If AB is one third of DE, and BC = 10, what is the length of EF?

4.

ABC ~ DEF. If AB = 12DE, and BC = 96, what is the length of EF?

5.

ABC ~ DEF. AB = x, BC = x + 2, DE = x + 1, EF = x + 4. What is the value of x?

6.

ABC ~ DEF. AB = 5, BC = 6, and CA = 7. If the length of EF is 4 more than the length of DE, what is the length of FD?