The Golden Ratio and Geometric Fibonacci Sequences

Reference > Mathematics > The Golden Ratio

After you've played around with Fibonacci Sequences for awhile, you notice (as was mentioned on the previous page) that the ratio of successive terms approaches a limit, and that limit is The Golden Ratio (or φ). It might occur to you to wonder (as I once wondered, long ago) if there was such a thing as a Fibonacci Sequence which is also ageometric sequence.

In other words, instead of the ratio of termsapproaching a limit, the ratio of terms is a constant.

This is fairly easy to figure out. In a geometric sequence, the terms would be a, ar, ar², ...

But since this is also a Fibonacci sequence, we must have the following:

a + ar = ar².

Hmm, it looks like we can drop out the a's - after all, if a is zero, the whole thing gets very uninteresting.

So we have: r² - r - 1 = 0.

"Hey!" you say, "Wait a minute! I've seen that before!"

That's right, you have! It showed up in our background of The Golden Ratio, it showed up in our continued fraction and our continued radical, and in our Golden Triangle calculations!

So I don't really need to tell you, do I?

If a Fibonacci Sequence is also a Geometric Sequence, the ratio between the terms is The Golden Ratio.

Except...hang on a second here. The quadratic equation I've given you has two roots, not one. In the past, we ignored the negative root, because we were dealing with geometric figures which had positive length sides. But is there any reason we couldn't have a negative ratio in our Geometric Sequence?

Of course not! So the ratio could also be:

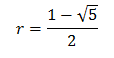
As one last thing to try, why don't you grind out the value of that expression. You should find that it equals -0.61803... That should look very familiar to you, because the portion of that number after the decimal point is identical to the decimal portion of The Golden Ratio. As an added bonus, that number is the negative reciprocal of φ!