The Golden Ratio in Trigonometry
Reference > Mathematics > The Golden RatioWhen we're talking about trigonometry, there are some angles we refer to as "special" angles. They are "special" angles because, with some very simple geometry, we can calculate their trig values. These special angles include: 0°, 30°, 45°, 60°, 90°, and multiples of these angles.
There is one angle, however, which we don't think of as a special angle, but really is quite special. It's a 36° angle. Let's take a look at a diagram together. The following is a 72-72-36 triangle, with an angle bisector drawn from one of the 72° angles.
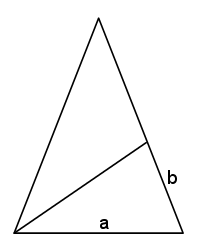
This triangle is often referred to as the "Golden Triangle," and we'll see why.
Since the line drawn is an angle bisector, it divides the 72° angle into two 36° angles. But wait! That means the smallest triangle is similar to the largest triangle, right? And themedium sized triangle is isosceles (both of its smaller angles are 36°).
Now, if you put all that information together, you know what you get? You get the following expression, which should look quite familiar to you:
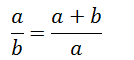
Does that look familiar? It should! That's the algebraic expression which we started with on the first page! That means that the ratio of the longer to the shorter side of this triangle is The Golden Ratio!
Sweet, isn't it?
"But what does that have to do with trigonometry?" You ask. Good question! If you split that triangle vertically down the middle, you get a 72-18-90 right triangle. And the ratio of shorter leg to the hypotenuse is 1/(2φ), which means the cos 72° = 1/(2φ)!
Do a little bit of manipulation, and you will discover the cosine of 36° is very interesting as well!
We'll come back to that a little later, but first, let's do some continuing fractions, by clicking Next below.
Questions
 The Golden Ratio in Nature
The Golden Ratio in Nature The Golden Ratio as a Continued Fraction
The Golden Ratio as a Continued Fraction

