Problems Involving Two Bodies

Frequently a problem will be given which involves the motion of two objects  with different speeds, accelerations, starting points, starting times and etc.  These objects will then move until one of them catches or meets the other.  Since each  problem of this  type will be different it is difficult to give concrete rules regarding their  solution. However, the following suggestions may give you some help in  attacking the problems.  List everything known about the motion of the  objects.  You will need a separate list for each object.  Frequently it will be necessary to give a quantity for one object in terms of the same quantity for the other.  For example, if the problem involved a car catching up with another car which had a head start of 500 ft you might give ΔX for one car as Z and ΔX for the other as Z + 500.  You may need to express more than one variable this way.  After listing all known quantities and expressing all unknown quantities as variables you should start writing equations.  You may end with a set of simultaneous equations which you solve using algebra.  Again you learn best by doing it.  Study the following examples and then work on assigned problems.

Sample Problem #1

Two boys are in a bicycle race.  John can accelerate with a constant acceleration of 0.5 and Paul can accelerate with a constant acceleration of 0.75 .  Paul gives John a head start of 5 seconds.
    (a)    Find how long before Paul catches John.
    (b)     Calculate the speed of both riders when Paul catches John.
    (c)    How far do they travel before Paul catches John?
                

Sample Solution #1

Note that this time we have expressed the two unknowns by variables.  Use equation 5 to express the distance traveled by both John and Paul in terms of a and t.  Then solve the set of equations you get for T and Z.

Combine these equations to obtain

You should show that the solution to this equation is T = 27.3 s and Z = 186 m.  Therefore Paul catches John 27.3 seconds after John starts.  When they are even both will have traveled 186 m.  You could check your work by using John's time (22.3 s) and acceleration (0.75 ) to see if his distance is also 186 m.

Graphical Analysis

Frequently a graph can be a useful tool in studying the motion of an object.  The graphs do not always need to be constructed.  Often a good sketch will help in the analysis of the motion.  The two graphs which are generally most likely to be useful are graphs of position vs. time or speed vs. time.  The following facts should be kept in mind:

1. In a position vs. time graph the slope of the line at any point represents the speed at that instant.
2. In a speed vs. time graph the slope of the line at any point represents the acceleration of the object at that instant.
3. In a graph of speed vs. time the area between the line and the time (horizontal) axis between two points is the distance traveled by the object between those two times.
4. In an acceleration vs. time graph the area between the line and the time axis is between two points is the change in speed during that time interval. The use of graphs in solving problems is shown in the problems below.   Study these problems carefully and be alert for places in your problem solving where these techniques can be helpful.

Sample Problem #2

Represent the motion of the two boys in problem 7 by graphs and use the graphs to solve the problem.

Sample Solution #2

The most useful graph is frequently the graph of speed vs. time since both acceleration, speed and displacement can be obtained from it.  Sketch a graph showing the motion of both objects on the same set of axes.

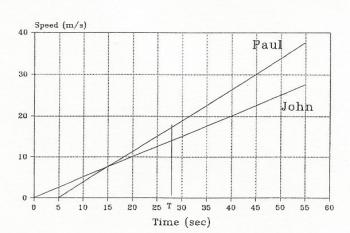
^{Figure 1.4.1}

Study Figure 1.4.1 carefully.  The line representing John's motion has a constant slope of 0.5 starting at the beginning of the motion.  The line representing Paul's motion remains at zero until 5 s have elapsed and then has a constant slope of 0.75 .  John's speed at any point will is the slope multiplied by the elapsed time (0.5T).  Paul's speed will be zero until 5 s have elapsed and after that will be 0.75(T - 5).  The point at which the two lines cross is the time when the two boys have the same speed, it is not the point at which they have moved the same distance.  Before that point in time John is moving faster than Paul and is pulling ahead of him.  After that time Paul is moving faster than John and is gaining on him.  Paul will catch up with John when the areas under the two lines are equal.  The two areas involved are both triangles.  The area for John is a triangle with a base T (where T is the time they come together) and  height of 0.5T.  The area for Paul's motion is a triangle with a base of (T - 5) and a height of 0.75(T - 5).  Since we wish to know when the boys are at the same distance from the start we set the two areas equal to obtain.

Note that this is the same  equation  which was obtained by different reasoning the first time we solved this problem.  The rest of the problem proceeds much as before.  We really have introduced nothing new but have only shown a different way of seeing the motion.

Sample Problem #3

You have a car which can accelerate from 0 to 60 mph (88 )  in seven seconds.  A car passes you just as you start up from a stop light.  The speed limit is 60 mph.  Doing your transmission no favor, but obeying the law: 
    (a)    how long will it take you to catch the other car?
    (b)    how far will you have gone?

Sample Solution #3

It is probably best in a problem such  as this to express all speeds and distances in and ft.  Since 60 mph is 88 , 40mph must be 58.7 .  Your car can accelerate from 0 to 88 in 7 s so its acceleration must be 88/7 = 12.6 .

The motion of the two cars is shown in Figure 1.4.2.

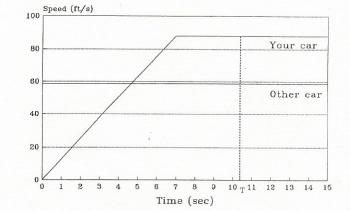
^{FIGURE 1.4.2}

Please note that this problem has an added complication, not only does it involve the motion of two objects, the motion of one of them (your car) has to be divided into two parts.  The other car has a steady speed of 58.7 as showed by the horizontal line.  Your car starts at rest and has a constant acceleration of 12.6 for seven seconds and then travels at a constant speed of 88 until it catches the other car.  You will catch the other car when the areas under the two curves are equal.  The area under the curve for the other car is a rectangle with a base of T (the time you catch him) and a height of 58.7 (his speed).  The area under the curve for your car is the sum of two areas: a triangle  with a base of 7 seconds and a height of 88 , and a rectangle with a base of (T - 7) seconds and a height of 88 .  Setting these two areas equal gives:

The student can show that the solution to this equation is T = 10.5 s.  Use this value of T to obtain the distance moved by either of the cars which will come out to be 616 ft.

1.

Two motorcycles are at rest and separated by 24.5ft. They start simultaneously in the same direction, the one in the back having an acceleration of 3.00 ft/sec² and the one in the front with an acceleration of 2.00 ft/sec². How long does it take for the faster cycle to overtake the slower? How far does the faster machine go before it catches up? How fast is each cycle going at this time?

2.

Superman is standing in a window of a building 100ft above the street. A baby hurtles past, having fallen from a window 50.0ft higher. With what acceleration must Superman descend to catch the baby just before it is too late?

3.

A balloon rises from the earth with a constant speed of 10.0ft/sec. A stone dropped from the balloon reaches the ground in 3.00sec. Find the height of the balloon at the instant the stone was dropped; the height of the balloon when the stone reaches the ground; the speed of the stone as it reaches the ground.

4.

A man is working in a basket attached to a balloon which is rising at a uniform rate of 32.2 ft/sec with respect to the ground, when he accidentally drops overboard a hammer which weighs 0.279lb. The hammer strikes the earth 10.0 sec later. What is the velocity of the hammer with respect to the ground at the instant it is dropped? How high was the balloon at the instant the hammer was dropped? If the balloon continues at a constant speed, how high will it be when the hammer strikes the ground?

5.

Who would win a 100yd dash, a runner who can cover the distance in 10.0sec, or an automobile which can accelerate to 60 mi/hr (88ft/sec) from rest in 16.0sec? By how much?

6.

An automobile and a truck start from rest at the same instant with the automobile initially at some distance behind the truck. The truck and automobile have constant accelerations of 4.0 and 6.0 ft/sec² respectively, and the automobile overtakes the truck after the truck has moved 150ft. How long does it take the auto to overtake the truck? How far was the auto behind the truck initially? What is the speed of each when they are abreast?

7.

A truck goes through a red light and continues to travel at 30mi/hr. At the instant the truck passes it at the intersection a waiting car assumes that the light has changed and starts up in the same direction as the truck with a constant acceleration of 12ft/sec². Two seconds later a motorcycle officer leaves the intersection with a constant acceleration. If he wishes to catch both offenders, what should be the value of his acceleration to reach the car just as it is passing the truck?