Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!

One of the first things I do every year when I realize that the new year upon us...
...no, not New Year's resolutions.
No, I always reduce the new year to its prime factorization. Why? Because sometimes I write competition math problems involving the school year, and so it's nice to know how the number factors.
In case you were wondering, 2016 = 25327.
It's also, by the way, 25 less than 211. That's right - in 32 more years, the year number will be a perfect 11th power.
And if you want to verify that without using a calculator:
25327 + 25 = 25(327 + 1) = 25(63 + 1) = 2526 = 211.
Obviously, even when I'm on school vacation, my math mind doesn't shut down. In fact, I just spent a good part of a day writing a math unit that some of my high school students will be working on later on this year: Probability. This unit covers essential concepts like dependent and independent events, mutually exclusive outcomes, complementary outcomes, and compound events. There may eventually be a second probability unit that delves into more topics, such as conditional probability. For now, if you're looking for basic concepts, this is a good starting point.
Meanwhile, a unit on Pythagorean Means has also been added to the site.
It seems that some of you haven't left behind your math brains while on Christmas vacation, either. Professor Puzzler has fielded a handful of math-related questions while on vacation:
- Why Can't I Divide by Zero?
- Why Does Cryptology Exist?
- What Are Telescoping Series?
- What Does the Upper-Case Pi Mean?
Thanks for all the great questions!
Happy 211 - 25,
Douglas Twitchell
TPS Admin
Medhavi wants to know, "Why can't I divide by zero?"
That's an excellent question, Medhavi. When I'm teaching, I tell my students that dividing by zero is illegal, immoral, and socially unacceptable, and if they do it, I'll have them arrested and thrown into math prison.
I also tell them that dividing by zero makes math problems explode.
But that's just me being silly; it doesn't really answer the question of why it's illegal. I'll try to give you a couple different ways of looking at the question, in hopes that at least one of them will help you feel confident that there really are good reasons to not allow it.
Division as the Inverse of Multiplication
First, you can think of division as being the inverse of multiplication. Let me show you what I mean by example:
14/2 = 7, because 7 x 2 = 14
32/4 = 8, because 8 x 4 = 32.
So now let's apply that to a "division by zero" problem:
15/0 = ?, because 0 x ? = 15.
Ah...in order to solve the division problem, you have to solve the multiplication problem. If you want to know what 15 divided by 0 is, you have to figure out what number you need to multiply 0 by to 15. And the answer is?
I'm waiting...
You can't find one, can you? Nope! Because anything times zero is just zero, so you can never make it work out to 15.
It's just plain silly to think you could.
Division as Repeated Subtraction
Here's another way of looking at division: 14/2 = 7 because you can subtract 2 from 14 seven times before you reach zero.
If that's the case, what is 20/0? Well, how many times can you subtract zero from 20 before you reach zero? WHAT? What kind of a question is that? You can't ever reach zero by subtracting zero from 20, no matter how many times you do it!
It's just plain silly.
Real World Division
What does division mean in the real world? 100 divided by 5 could be understood like this: If you have 100 marbles and you divide them into 5 equal groups, how big is each group? The answer to 100/5 is 20, because each group of marbles has 20 marbles in it.
100/2 = 50, because if you divide 100 marbles into two equal groups, there are 50 marbles in each group.
Great. So what is 100/0? Well, you find that by dividing 100 marbles into zero groups.
What? How do you do that? How in the world can you take 100 marbles and split them up into zero groups? That's just silly!
It's tempting to say, you do it by taking a stick of dynamite to your marbles, so there won't be any marbles.
But that's not dividing it into zero groups. That's dividing it into billions of groups (pieces), and each piece is really, really tiny.
So, you just flat out can't do it.
Dividing Zero by Zero
But what about dividing zero by zero? Can't you divide nothing into no groups?
I would argue that you can't. You can divide it into any positive number of groups, and each group has zero marbles in it, but it's meaningless to suggest that you're going to "split" something into zero groups.
But in case you disagree with me, let's go back to our definition of division as the inverse of multiplication:
0/0 = ?, because 0 x ? = 0.
Can you find a number to put in place of the question mark? Yes! The problem isn't that you can't find a number that works; the problem is that any number will work. 0 x 1 = 0; 0 x 2 = 0; 0 x 3 = 0, etc.
We can't give an answer to the division problem, because there isn't just one answer to the multiplication problem. We end up with the a similar issue if we treat it as a repeated subtraction problem.
Since there's no way to give one answer, we reject the notion of giving any answer. Division by zero is illegal, immoral, and socially unacceptable. And if you do it, we'll throw you in math prison.
We might even chain you to a dodecahedron and whip you with a Moebius strip.
Ayako asks, "Why does cryptology exist?"
Cryptology is "the study of codes, or the art of writing and solving them."
So why does that study exist? The short and simple answer to that question is: Because human beings are capable of dishonesty and treachery.
What do I mean by that? Well, if humans were always fair and honest, we'd never need to encode things. Codes are used to keep secrets from people we don't trust.
Have you ever noticed that whenever you go online to check your bank statements, or make a purchase, or pay your credit card bill, you're on a site with "https" as part of the web address, instead of "http?" That "https" means that your connection to the site is encrypted. And it's a good thing that it is! You are sending personal banking/financial information to the website. If the connection wasn't encrypted, then other people could "eavesdrop" on your conversation and get all kinds of information they shouldn't have: your bank account number, your credit card number, and login information that they could use to access your credit history, or even make purchases using your money.
Of course, if there weren't dishonest people in the world, you wouldn't care if people had your credit card number, because they would never use it. You wouldn't care if they had access to your bank account, because they would never take advantage of the information.
But people can be dishonest, so we need to encrypt things we want to protect.
Codes have also been used in wars. In World War II, the Germans had their Enigma machine, which was used to encode messages. Each day there would be a "key" that could be used to decode the messages, as long as the person receiving the message also had a matching Enigma machine.
The allies worked for months trying to break the enigma code, because they knew that if they could access the messages being sent, they would know the Germans' plans, and be better able to counteract their strikes.
Of course, there are uses for codes that are more benign than these examples. Take this, for example:
"Nvvg nv zg mllm zg gsv hvxivg xofy slfhv gl svok kozm Nzc'h hfikirhv yrigswzb kzigb."
You have no idea what that means, but if you go to our "Backwards Alphabet" code page, you will discover that this secret message was not designed to protect financial information, or steal information, or plan any war tactics.
Thanks for asking!
Sincerely,
Surihvvru Sxccohu (can you decode my name?)
Anonymous asks, "What is telescoping sequence?"
Well, Anonymous, it's probably better to say "telescoping series," because the adjective "telescoping" refers to something that happens when you combine the terms, not the individual terms themselves. So I'll reword your question to "What is a telescoping series?"
First of all, when you see the phrase "telescoping," you shouldn't think of a normal telescope that you might see in an observatory. Instead, you should think of a spyglass, like this:

A telescoping series is like a spyglass, in that it looks long, but can be collapsed into something very small. When a spyglass is collapsed, the middle parts disappear, and all that's left is the two ends. The same is true of a telescoping series.
Here's an example. Consider the following series:
1/2 + 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 + 1/110
This looks rather intimidating to calculate if you don't have a computer or calculator to do the work for you; that's going to have one very large least common denominator!
But did you notice a pattern to the denominators? you could rewrite each of the fractions like this:
1/n(n + 1) (for example, 1/42 = 1/6(6 + 1).
But 1/n(n + 1) can also be written as follows: 1/n - 1/(n + 1). (Don't believe me? Do the algebra to combine the two fractions, and you'll see that it's true! Or use your calculator to test it out on a few values.)
So why is that useful to write the terms that way? Because it causes the series to "telescope" or collapse. Watch what happens when we rewrite each of the fractions this way:
1/2 = 1/1 - 1/2
1/6 = 1/2 - 1/3
1/12 = 1/3 - 1/4
1/20 = 1/4 - 1/5
and so forth, down to
1/110 = 1/10 - 1/11
Now what happens if you add all of those together?
(1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ... + (1/10 - 1/11)
Notice that you have a positive 1/2, and a negative 1/2, which cancel. Similarly, the 1/3, 1/4,1/5, ect. fractions cancel out. Everything cancels out except the 1/1 at the beginning, and the 1/11 at the end.
So the sum is 1/1 - 1/11 = 10/11.
And I was able to calculate the sum in my head, without ever picking up a calculator, or writing on a sheet of paper. Obviously, telescoping series are pretty cool, and they can be useful in various areas of higher mathematics.
Thanks for asking!
Professor Puzzler
Shawna from Michigan asks, "The upper case sigma symbol is used for summation, but I've also seen the upper case pi symbol used in a similar way. What does that mean?"
Hi Shawna. The answer is pretty short and straight-forward. The pi symbol, when used that way, means multiplying a set of numbers (instead of adding them).
If you're wondering why pi is used, the reason is simple; it's the same reason we use sigma for sums. S for sigma, S for sum. P for Pi, P for product.
Here's an example; take a look at this expression:
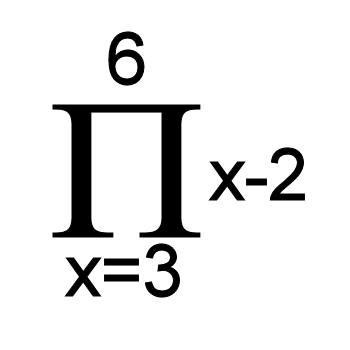
This means that we multiply together all the numbers we get by plugging in x = 3, x = 4, x = 5, and x = 6.
The numbers are:
3 - 2 = 1
4 - 2 = 2
5 - 2 = 3
6 - 2 = 4
So the product is 1 x 2 x 3 x 4 = 24
Of course, that was a fairly simple problem, and they can get a lot more complicated (interesting) than that. But that will be sufficient to answer your question, I think!
Professor Puzzler

