Since it's almost the new year, this image (click the image for a larger view) is making the rounds on facebook again, and everyone is reading it and saying, "WHAT? How does that work out to $667.95?"

The answer is, it doesn't. It works out to exactly what you thought it would work out to: 365 pennies, or $3.65. Unless it was Leap Year, and then it would work out to $3.66. Not terribly hard math.

However, even though "a penny a day" is what they said, "a penny a day" is not what they meant. How do I know that? I'll show you in just a minute.

What they meant was, on January 1st you put in one penny. On January 2nd, you put in two pennies. On the 3rd, three pennies. And so on, until December 31st, when you put in 365 pennies, because it's the 365th day of the year.

How do I know that's what they meant? Because there's a really nice formula to calculate the sum of the first n integers:

Sum = n(n + 1)/2

In this case, n = 365, so the sum is:

Sum = 365(365 + 1)/2 = 66,795.

And that's how I know that's what they meant - because if that's what they meant, the math works out correctly to $667.95.

And by the way...if it was leap year?

Sum = 366(366 + 1)/2 = 67,161, or $671.61.

So yes, this will work out to save you a pretty good sum of money by the end of the year. Maybe enough to pay a month's rent, depending on where you live!

Of course, it's not as good as doubling the number of pennies each day; that would save you a boatload of money over the course of a year:

1 + 2 + 4 + ... + 2ⁿ = 2^{n + 1} - 1

So: 1 + 2 + 4 + ... + 2³⁶⁵ = 2³⁶⁶  - 1 = 1.5 x 10¹¹⁰.*

Actually, scratch my last comment; that's not a boatload of money. If a penny's volume is 0.35 cm³, or 0.00000035 m³, that's a volume of 5.25 x 10¹⁰³ m³. Considering the volume of the sun is 1.4 x 10²⁷ m³, I don't think you're going to fit those pennies in a jar, a boat, or even all the planets of the solar system. Maybe we should just stick to the original plan.

Incidentally, there's also a "Dollar a Week Challenge" in which you save one dollar the first week, two dollars the second week, and so on for an entire year. It sounds like a lot more, since you're saving a dollar instead of a penny, but there are only 52 weeks in the year, so it works out like this:

Sum = 52(52 + 1)/2 = $1,378, which is only a litte more than twice the penny challenge.

If you wanted to get really interesting, you could do a "Dollar Square Weekly Challenge," which would look something like this:

In the first week, you save 1² = 1 dollar.
In the second week, you save 2² = 4 dollars.

And so forth. It turns out, there's a nice formula for the sum of squares as well:

Sum = n(n + 1)(2n + 1)/6

Sum = 52(52 + 1)(2 x 52 + 1)/6 = $48,230. That's a lot of money! How would it compare to a Penny Square Daily Challenge?

Sum = 365(365 + 1)(2 x 365 + 1)/6 = 16,275,715 pennies, or $162,757.15. So even though the Dollar Challenge saves more than the Penny Challenge, the Penny Square Challenge saves more than the Dollar Square Challenge.

It would be interesting to see how many weeks you'd have to do the Dollar Square Challenge in order for it to surpass the Penny Square Challenge for a year. I'll leave that do the reader to figure out!

* This formula is actually for a leap year. Since the first term of the sequence is 2⁰, the 366th term is 2³⁶⁵.

It's my yearly tradition to take the number for the new year and see if I can find interesting mathematical novelties about the new year. 

The first thing I always do is check the prime factorization. It turns out 2017 is a prime number. So that's something novel, yet not extremely unusual, since there are an infinite number of primes. The previous prime year was 2011, and the next one is 2027.

Incidentally, since it is a prime, and it is one more than a multiple of four, Fermat's theorem on the Sums of Two Squares gives us an interesting conclusion: 2017 can be written as the sum of two perfect squares.

The two squares, in case you were wondering, are the squares of 9 and 44. 2017 = 9² + 44².

Can it be written as the sum of three perfect squares? Yes it can, as follows:

12² + 28² + 33²
18² + 18² + 37²
21² + 26² + 30²

For those who enjoy numerology, multiply the two numbers being squared in the second row above (18 and 37), and you'll get a beastly number (666). And you thought 2016 was bad.

Not that this is terribly unusual, but 2017 can be written as the sum of two palindromes:

2017 = 1331 + 686

Of course, I also like to see if I can find a ridiculously ugly way of writing it, and this year's looks like this:

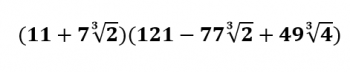
That looks appalling, I know. You're welcome to multiply it out, and you'll see that it works out to 2017. If you're wondering how I came up with that nasty thing, I did it by noticing the following:

2017 = 1331 + 686 (as mentioned above)
2017 = 11³ + 2×7³
2017 = 11³ + (7×2^1/3)³

And then it was just a matter of using the sum of cubes factoring rule:

a³ + b³ = (a + b)(a² - ab + b²)

It's interesting that 2017 can be written as a perfect square plus twice another perfect square (2017 = 37² + 2×18²) and it can be written as a perfect cube plus twice another perfect cube (2017 = 11³ + 2×7³).

Happy New Year!

PS - if you write your dates as m/d/y, you'll be looking forward to July 10, 2017, which is 7102017, another palindrome. Otherwise you'll be looking forward to October 7, 2017.

One of the first things I do every year when I realize that the new year upon us...

...no, not New Year's resolutions.

No, I always reduce the new year to its prime factorization. Why? Because sometimes I write competition math problems involving the school year, and so it's nice to know how the number factors.

In case you were wondering, 2016 = 2⁵3²7.

It's also, by the way, 2⁵ less than 2¹¹. That's right - in 32 more years, the year number will be a perfect 11^th power.

And if you want to verify that without using a calculator:

2⁵3²7 + 2⁵ = 2⁵(3²7 + 1) = 2⁵(63 + 1) = 2⁵2⁶ = 2¹¹.

Obviously, even when I'm on school vacation, my math mind doesn't shut down. In fact, I just spent a good part of a day writing a math unit that some of my high school students will be working on later on this year: Probability. This unit covers essential concepts like dependent and independent events, mutually exclusive outcomes, complementary outcomes, and compound events. There may eventually be a second probability unit that delves into more topics, such as conditional probability. For now, if you're looking for basic concepts, this is a good starting point.

Meanwhile, a unit on Pythagorean Means has also been added to the site.

It seems that some of you haven't left behind your math brains while on Christmas vacation, either. Professor Puzzler has fielded a handful of math-related questions while on vacation: 

• Why Can't I Divide by Zero?
• Why Does Cryptology Exist?
• What Are Telescoping Series?
• What Does the Upper-Case Pi Mean?

Thanks for all the great questions!

Happy 2¹¹ - 2⁵,
Douglas Twitchell
TPS Admin