Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Here's a fun question regarding an upcoming snowstorm:
"4 to 8 plus 4 to 8 equals 8 to 16, right?"
This is in reference to a prediction that tomorrow there will be 4 - 8 inches of snow, and then tomorrow night there will be 4 - 8 inches of snow. The questioner is suggesting that this means there will be a total of 8 - 16 inches of snow.
It seems reasonable, right? Except we're all pretty sure we're not going to see anywhere near 16 inches of snow in the next 48 hours. So why can't we just add these two ranges together?
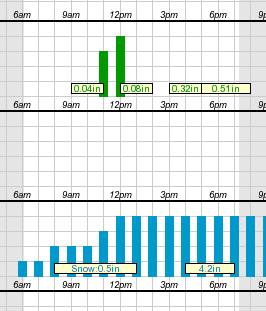
Meterologists have a LOT of unknowns they have to deal with (and I'm not a meteorologist, so I'm not going to pretend I know even a tenth of the variables they deal with). But what I do know is that one of the broad uncertainties is when a storm will pass through. If you look at the chart here (taken from an actual hourly forecast on the National Weather Service website), you'll see that they don't actually know when the storm will start; the snowfall bars begin (with low probability) at 6:00 AM. It's not until noon that they're saying with confidence, "We'll have snowfall by now."
So hypothetically, if the snowstorm starts at 6:00 AM, and goes all day, maybe we'll get 8 inches of snow during the day. But if that happens, the storm will be mostly over by evening, and maybe we'll get 4 inches overnight.
On the other hand, if the storm doesn't start until noon, maybe we'll get 4 inches during the day. But then the storm will last longer into the night, and maybe we'll get 8 inches overnight.
What I've just described is a scenario in which we get a maximum total of 12 inches. But if we were to break it down by how much falls during the day and how much falls at night, we'd have to say "4 - 8 during the day" and "4 - 8 during the night" - even though we feel confident that the storm won't give us more than 12 inches total.
What we're seeing is that a portion of the snowfall could come during the day, and it could come at night. Since we don't know when, it gets listed in both time periods.
Watch the forecasts and see how they line up from storm to storm, and you'll see what I mean: if the daytime forecast is accurate, the overnight forecast will likely be overkill. And vice-versa. Of course, we don't always notice this, because as the storm gets closer, the meteorologists are able to refine their models better.
Then we just whine that the meteorologists have been "hyping up the storms." :D
As I mentioned before, there are undoubtedly many many more variables that I'm not considering, but my purpose here was to show wny you can't just sum the ranges to get a total.
Maizi from Norwich asks, "Four positive whole numbers add up to 84 One of the numbers is a multiple of 17 The other 3 numbers are equal. What are they?"
Hi Maizi, as is my custom with math problems, I'm not going to answer your question; instead I'm going to invent a similar problem and show you the technique for solving it. This will allow you the satisfaction of solving this particular problem on your own. So here is my problem:
Five positive whole numbers add up to 97, and one of them is a multiple of 19. The other four numbers are all equal. What are they?
First, we consider that if we add together four equal numbers, the result must be a multiple of four. For example, 7 + 7 + 7 + 7 = 28, or 11 + 11 + 11 + 11 = 44.
Algebraically, we'd say that n + n + n + n = 4n.
So this means that if we subtract the first number (the one that's a multiple of 19) from 97, we will have a result that is a multiple of 4.
What could the first number be? 19, 38, 57, 76, or 95. Any other value is larger than the sum of 7, which is not possible if all the integers are non-negative.
Based on this, we can find all possible sums of the other four numbers, by subtracting each of the numbers above from 97:
97 - 19 = 78
97 - 38 = 59
97 - 57 = 40
97 - 76 = 21
97 - 95 = 2
Remember what I said earlier? The other four numbers must add to a multiple of 4. The only one of those sums above that is a multiple of 4 is 40. Therefore, we conclude that the first number is 57, and the other four numbers are each 10 (because 40 / 4 = 10).
I hope that's helpful; good luck with your version of the problem!
"Are there any tricks that can help you easily factor three digit numbers (without using a calculator)?" ~Jay
Hi Jay, I assume you're talking about tricks besides the normal divisibility rules (for example, if the digits add to three, the number is a multiple of three, if it ends in 0 or 5 the number is divisble by 5, etc). If you're not familiar with those rules, you might want to take a look at this unit here: Divisibility Rules.
Beyond that, there are some tricks that sometimes help. Here's my favorite. Let's say you wanted to factor the number 483. Here's what I would do:
- Multiply the first and last digit: 4 x 3 = 12
- Find two numbers that multiply to 12 and add to the middle digit (8). The numbers are 6 and 2 (6 + 2 = 8 and 6 x 2 = 12).
- Now rewrite the number using those two numbers we just found: 483 = 460 + 23 (the tens place got split into two pieces using our numbers, and the entire number was rewritten as a sum of two numbers).
- Now factor the result: 460 + 23 = 23(20 + 1) = 23 x 21.
- Finish factoring: 23 x 7 x 3
Unfortunately, this doesn't always work. For example, it won't work for 648, because you can't find two numbers that add to 4 and multiply to 48. But maybe if we can find a way of regrouping this number, we might get around that. My first thought is to pull out one of the "hundreds" and put it into the tens place. So we're thinking of 648 as being rewritten 5(14)8. Now we do 5 x 8 = 40, and realize that our two numbers must be 4 and 10 (4 + 10 = 14 and 4 x 10 = 40). So we rewrite the number: (600 + 48 = 24(25 + 2) = 24 x 27. Then we just finish the prime factorization from there.
If the number is one of those special numbers (like 483) that can be factored without regrouping, it's a straightforward, foolproof process. But if the number has to be regrouped, it requires a bit of intuition to work it out. However, if you don't have a calculator, it might be worth doing!
Thabang from Lesotho writes, "how do we rationalize a denominator consisting of a cube root with another constant added to it or subtracted from it?"
Good morning, Thabang, and thank you for your question. This is actually something I don't remember ever seeing before, so I had to give it some thought before answering.
What you're looking for is, how do we rationalize the denominator, if the denominator is something like "The cube root of three, plus two" or "the cube root of three, minus two"?
In order to solve this, it's important to remember two factoring rules you may have learned in an Algebra class:
x3 + y3 = (x + y)(x2 - xy + y2)
x3 - y3 = (x - y)(x2 + xy + y2)
Let's say your denominator is the cube root of three, plus two. Then I'm going to do the following substitutions:
Let x = the cube root of three, let y = 2.
Now your denominator is x + y, and if you multiply the numerator and denominator of the fraction by (x2 - xy + y2), you will have turned the denominator into x3 + y3 = 3 + 8 = 11, which is rational.
That was using the first factoring rule shown above. If the denominator had a subtraction (the cube root of three, minus two), we'd just use the second factoring rule, and multiply by (x2 + xy + y2).
Thanks again for asking, Thabang.
Navya asks: "Why do we have names for numbers?"
There are two answers to this question. The first answer is: because it's impossible to talk about numbers verbally unless you have names for them. If we didn't have the names "one", "two", "three" and so forth, how would we ever say "I have five apples"?
That explanation is sufficient for why we have names for the numbers from zero to nine, but it's not sufficient for numbers like eleven, twelve, and so on. After all, if we didn't have the name "eleven", we could still say the number by saying "one one."
Thus, we would count like this (starting at ten): "one zero, one one, one two, one three..." and so forth.
And in some cases, that would be quicker. The name "eleven" has three syllables, while "one one" just has two. Even worse would be a number like "three thousand, four hundred, sixty three" which takes nine syllables instead of the four syllables required for "three four six three".
So, since the number names aren't always quicker to say than just reciting off the digits, why do we bother? The answer is that using number names allows us to get an immediate order-of-magnitude sense for how big the number is. Look at it this way - if I say "seven million, two hundred twenty three thousand, four hundred twelve," the moment I said "seven million" you had a very good sense for how big that number is. But if instead I had said "seven two two three four one two" you would not have any way of determining the number's magnitude until I was all done reciting the digits, and you knew how many digits there were. And if you lost track of how many digits there were, you still wouldn't have a good sense for how big the number is!
So number names are very helpful for order-of-magnitude sense of the size of a number.


