Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Bramasta asks, "Is it possible to have a number that is a multiple of 2 but not a multiple of 4 and is a perfect square number?"
That's a great question, Bramasta, and I'm guessing you've tried a few examples, and decided the answer is probably "no," but you're wondering if we can know it for sure.
Another way of describing "a number that is a multiple of 2 but not a multiple of 4" is to say "a number which is two more than a multiple of four." So if we can show that no perfect squares are two more than a multiple of four, we'll have answered your question. Ready?
If Y is a perfect square, that means its square root, X, is an integer. Consider that X must be either even or odd. In other words, for some value K,
X = 2K or
X = 2K + 1
Since Y = X2, Y = (2K)2 or Y = (2K + 1)2. Multiplying these out gives us the following:
Y = 4K2 or Y = 4K2 + 4K + 1 = 4(K^2 + K) + 1
Notice that in the first case, Y is a multiple of 4, and in the second case, it's one more than a multiple of four. In no case do we get a result that is either 2 more than a multiple of 4 or 3 more than a multiple of four. So we've actually proved MORE than you asked; if a number is either 2 more or 3 more than a multiple of 4, we can emphatically declare that it is NOT a perfect square.
Thanks for asking!
This blog post is about the "Monty Hall Problem" - which you can find a blog post about here: Ask Professor Puzzler about the Monty Hall Problem, and a game simulation here: Monty Hall Simulation.
Larry from Louisiana writes: "Relating to the 3 door problem the answer given is just plain silly. Consider everything the same except you now have two players, one selects door one and the other selects door two. Now door three is shown to have a goat so, according to the given solution both players switch doors and each now has a 66% chance of winning? This may be possible in the new math but it is not in the old math that I learned."
Hi Larry, thanks for the message.
Before responding, I'd like to mention, in case anyone is confused by the "goat" part of your message, that in different versions of the game either two doors are empty, or they contain a donkey, or a goat, or some other silly prize. In the blog post here on this site I refer to the door as being empty, but to make my answer consistent with Larry's comment, I'll refer to the empty doors as containing a goat.
I'd also like to add that when I'm writing math problems for math competitions, my proofreader and I always comment - half joking (which means half serious!) that we hate probability problems, and wish we didn't have to write them. Probability problems can be very tricky, and it's easy to overlook assumptions we make that completely change our understanding of the problem.
In the case of the Monty Hall problem, there are a couple hidden assumptions that can be overlooked.
- Since the game show host always shows the contestant an empty door, that implies (even though this is not always stated outright) that he knows which door contains the prize. His choice is dependent on his own knowledge.
- Since only one door has been opened, the game show host has a choice, and it is always possible for him to choose an empty door.
It may be helpful to think of the game show host as a "player" or "participant" in the game. If the game show host cannot operate under the same conditions within the game, it is not the same game.
The game you proposed is an entirely different game with conditions that violate the conditions stated above. Specifically, even though in your stated scenario the game show host shows a goat, we need to understand that it is not always possible for him to choose a goat door; if the contestants have each picked a goat door, there is no door left for him to show except the one with the prize. In other words, the game show host's role is completely different. While he still knows which door contains the prize, he no longer has a choice, and (just as importantly) it is not always possible for him to choose an empty door. Another way of saying this: in your game, the host is no longer a participant in any meaningful way.
Since your game has conditions that violate the conditions of the Monty Hall Problem, it is not the same game, and we shouldn't expect it to have the same probability analysis. In fact, it doesn't, and you correctly observed that it wouldn't make sense for it to work out to the same probabilities.
I would encourage you to try out the simulation I linked at the top of this page; if you're willing to trust that I haven't either cheated or made a mistake in programming it, you'll see that the probability really does work out as described. And if you don't want to put your trust in my programming (which is fine - I think it's good for people to be skeptical about things they see online!), I'd encourage you to get a friend and run a live simulation. The setup looks like this:
- Take three cards from a deck, and treat one of them as the "prize" (maybe the Ace of Spades?)
- You (as the game show host) spread the three cards face down on the table. Before you do, though, remember that you're going to have to flip one of the cards that isn't the Ace of Spades, which means you need to know which card is the Ace of Spades. So before you put the cards on the table, look at them.
- Now ask your friend to pick one of the cards (but don't look at it).
- Since you know which card is the Ace of Spades, you know whether he has selected correctly. If he's selected correctly, you need to just randomly pick one of the other two cards to show him. If he hasn't picked the Ace of Spades, you know which one is the Ace of Spades, so you show him the other.
- Now ask him if he wants to switch. You'll need to agree beforehand whether he'll always switch or never switch, but he should be consistent and make the same choice each time.
- Do steps 2-5 about 100 times. If your friend always chooses to switch, you'll find that he wins about 2/3 of the time, while if he never switches, he'll win about 1/3 of the time.
I've had classes of high school math students break up into pairs and run this simulation, and the results always come out as described above. Happy simulating!
William from Arizona asks, "Myself and a fellow math teacher of 20+ years each got into a discussion about extraneous solutions for a particular problem. The problem is this: 1/(x-a) = x/(x-a) The provided answer to this problem is that x = a is always an extraneous solution. However, when you solve it using the LCD method to multiply both sides, the x = a solution candidate does not present itself. (x-a) * 1/(x-a) = x/(x-a) *(x-a) 1 = x cancelling x-a The only candidate after cancelling is x = 1. The counter argument was that you solve by cross multiplying and setting equal getting: x - a = x(x - a) x - a = x^2 - ax 0 = x^2 - ax - x - a 0 = x^2 - (a+1)x - a Using quadratic formula: x = a or x = 1 therefore, x = a is extraneous. Using the cross multiply method, I run into x = a and need to call it extraneous. Using LCD multiply to both sides, it doesn't present as a candidate. So, is it true to say x = a is always an extraneous solution? Thank you for considering"
Hi William, thanks for asking. This is an interesting question. An extraneous solution is generally defined as "a solution to a transformed equation which is not a solution of the original equation." So, for example, if you square both sides of an equation, you've transformed it, and therefore you've introduced the possibility of solutions that might not be solutions to the original equation.
In this case, the transformation that produces an extraneous solution is cross multiplying, which removes the (x - a) from the denominator (and therefore including x = a in the domain).
So an extraneous solution is a solution that arises because of a transformation. If the transformations you performed did not result in a new equation that has an expanded domain, then it doesn't produce extraneous solutions. In other words, no, I don't think you have an extraneous solution using the first method.
The phrasing here is odd; if x = 1 was an extraneous solution, you wouldn't say "x = 1 is always an extraneous solution." I suspect that what they're trying to say is, "it doesn't matter what the value of 'a' is; x = a will never be a solution." So I don't think they were trying to suggest that there's no way to avoid x = a as an extraneous solution, but rather that if it does arise as a solution, it is always extraneous, regardless of the value of 'a'.
As one last note, I'd like to point out that you can avoid using the quadratic formula in your second method:
(x - a) = x(x - a)
0 = x(x - a) - (x - a) //subtract (x - a) from both sides
0 = (x - a)(x - 1) //use the distributive property to rewrite the previous equation
x =a or x = 1
Thanks for asking!
Wesley asks, "I have been reading your answers to the corona virus questions and came across the term logistic curve. I am interested in the math behind them, and do not see how you can make a logistic curve unless one of two things. One, you take the inverse of an odd degree polynomial or two somehow you can incorporate the last y-value to influence the next x-value. I have come across this problem before and I would like to know if there is an alternate solution that can make a logistic curve an actual function of y in terms of x. If there isn't, thank you anyways for your time and effort."
That's a great question, Wesley. I like your thinking regarding odd degree polynomials. Odd degree polynomials do have an inflection point similar to a logistic curve. The problem with polynomial equations is that they don't have asymptotes. An asymptote is a straight line that the graph approaches without ever touching. A simple example of a graph with asymptotes is xy = 1. That graph gets closer and closer to the x and y axes, but never touches it.
A logistic curve has two horizontal asymptotes - one at the base of the curve, and one at the top. So a polynomial function (even an odd one) won't do the trick. What we need is an exponential function. Here's what you're looking for:
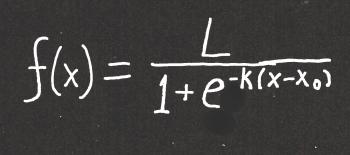
A "normal" exponential function might look something like this: f(x) = ekx. k controls how quickly the function "blows up" and x is the independent variable. Since we're thinking about virus spread, the independent variable is time - perhaps the number of days that have passed.
The logistic curve has elements of an exponential curve. It's interesting that the "e" is in the denominator, and also that it has a negative exponent - those two features sort of "cancel" each other out, because a negative exponent indicates taking the reciprocal. But it's the other stuff in the denominator with the e that makes this function's behavior interesting.
First, if x < x0, then the exponent of e is a positive number, and the denominator will be growing larger the further x is from x0. This results in a large denominator, which results in the value of the fraction approaching 0.
On the other hand, if x > x0, then e has a negative exponent, which means it is getting closer and closer to 0. This means the denominator is getting closer and closer to 1, and the function value is getting closer and closer to L.
This gives us our two asymptotes: y = 0 and y = L. Thus, 0 < f(x) < L.
And the point x = x0 is the point at which the function switches from blowing up to leveling off.
TO SUMMARIZE: in the logistic curve, k determines the rate at which the function grows, L represents the maximum value, and x0 represents the point in time at which the graph has its inflection point. In terms of a viral infection, L is the number of people who will be infected, and x0 is the time at which the number of new infections begins decreasing.
Wesley writes, "Is there a better way of factoring polynomials other than guess and check? For example: factoring 21x5 - 2x2 + 4x - 1, you probably will have to guess and check what goes in the parentheses. It could be (3x - something)(7x + something)(x - something)..., or, it could be something entirely different. Aside from the limited equations like difference of squares, or sum/difference of cubes, I would like to know if it is possible to not have to guess and check. If you do not know of a solution, thank you anyways for your time."
Hi Wesley, In addition to the rules that you mentioned, you can find a few more rules here, including sum/difference of odd powers, sum of even powers, grouping, and something I like to call aggressive grouping.
If none of those help, another tool that might help you out is something called the Rational Root Theorem. The rational root theorem says that if a rational zero to a polynomial exists, then written in simplest form p/q, p is a factor of the constant, and q is a constant of the highest order coefficient.
How does this help in factoring? Well, if p/q is a zero of the polynomial, then (qx - p) is a factor.
It's important to note that the statement above has a big "if" in it. It's possible that no rational roots exist. But if they do exist, this rule helps us out in our trial-and-error search by eliminating possibilities.
Let's take an example: 3x3 - 5x2 - 42x - 40 = 0.
The rational root theorem tells us that if this has rational roots, they are of the form p/q, where p is a factor of 40, and q is a factor of 3. Now, this still gives us a LOT of possibilities to consider, because p could be 1, 2, 4, 5, 8, 10, 20, or 40 (plus the opposites of all of those), and q could be either 1 or 3 (or their opposites).
So let's start with something that's not a fraction: Let's try 1, and see what happens. I'm going to do synthetic division on this. If you don't know how synthetic division works, you'll want to take a look at this explanation: How to do synthetic division.
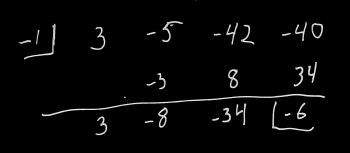
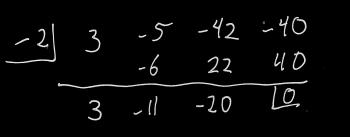
The next bit of good news is that we can use the values in our synthetic division to reduce the polynomial by the factor we just found: our polynomial can be rewritten as (x + 2)(3x2 - 11x - 20) (note the numbers at the bottom of our synthetic division - they are the coefficients of the reduced polynomial). To find our next factors we can use the techniques that we're familiar with on the factor 3x2 - 11x - 20, or we can continue doing synthetic division.
Of course, I cheated; I created a polynomial which I knew could be factored, but there's no guarantee that a given polynomial is factorable over real numbers, let alone rational numbers! Your polynomial, for example, has only one real root, and that one real root is not rational. If you had tried the rational root theorem on this, you would have tried 1, 1/3, 1/7, 1/21, and the opposites of all of those, only to find that none of them work. The good news is that because of the rational root theorem, you KNOW that you're done looking for rational roots.
So there are a few more tools for your arsenal; I hope something here was helpful!


