Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Laina asks for an explanation of the puzzle shown below.

The text reads: "THE BATTLE OF ENGLISH AND MATHEMATICS.
1 rabbit saw 6 elephants while going to the river.
Every elephant saw 2 monkeys going towards the river.
Every monkey holds 1 parrot in their hands.
How many animals are going towards the river???
Lets see who went to shcool..."
First, I doubt I'll be able to solve this, since I never went to shcool...
However, my answer is, simply, there is no solution, because there is not enough information given.
This is like a poor man's version of the "St. Ives" riddle. In case you don't know that riddle, it goes like this: "As I was going to St. Ives, I met a man with seven wives. Every wife had seven sacks, every sack had seven cats, every cat had seven kitts. Kitts, cats, sacks, wives, how many were going to St. Ives?"
With the St. Ives riddle, the narrator meets a man with seven wives. The word "meets" strongly implies* that the man with seven wives was going in the opposite direction.
Notice, though, that in our question here, it does not say that the rabbit "met" the elephants, only that he saw them, which could certainly mean that he overtook them as they were also on their way to the river. We simply don't know what the elephants are doing, and therefore there is not enough information to definitively answer the question.
I could end there, because the answer is indeterminate. However, I think it's worth exploring the question further.
The next question that arises is, how many monkeys are there? The two most common answers to this are two and twelve.
The first answer comes from assuming that each elephant saw the same two monkeys, and the second answer comes from assuming that each elephant saw two monkeys that none of the others saw. The most compelling argument for "two" as the answer is that the problem uses the word "every" instead of "each." The word "every" is a group word, implying the group as a whole did something. Thus, the group, as a whole, saw two monkeys. It's an interesting argument, but not all that convincing; grammarly states that each and every can be used interchangeable in some circumstances, and Cambridge Dictionary gives us such an example:
Each person has a bicycle.
Every person has a bicycle.
Both of these statements mean that there is a bicycle for each person. If we aren't going to assume that every person has the SAME bicycle (meaning, of course, that there's only one bicycle), then we can't assume that every elephant saw the same two monkeys.
Nor can we assume that every elephant saw two distinct monkeys that none of the others saw.
Therefore, there must be somewhere between 2 and 12 monkeys, inclusive, but the exact quantity of monkeys is unknown. Giving us, once again, an indeterminate answer.
There was another argument I saw for two monkeys - some people were saying, "since the problem doesn't state explicitly, implicit rules apply, making it two." Implicit rules? What is that? Is it just a fancy way of saying, "Since they didn't specify, I get to pick whichever makes the most sense to me, and call it the 'default' meaning."?
Regarding the parrots, it's interesting to me that the people who present the "each vs. every" argument are inconsistent; If "every elephant saw two monkeys" means that the group as a whole saw two monkeys, then "every monkey holds one parrot" means that the group as a whole is holding a parrot, and there is one parrot, instead of two parrots. It seems to me that you can't have it both ways.
Finally, there really is no battle between English and Mathematics. I've been hired to write competition math problems in at least three different states, and I can tell you that English and Mathematics work side-by-side to make a good problem. Ambiguity in the use of English makes the problem unsolvable. If this problem showed up in any math competition anywhere, the appeals committee for the competition would be inundated with appeals written by students arguing for different answers. The appeals committee would have to accept multiple answers or throw the problem out entirely (I saw this happen just a couple weeks ago at a state math competition; because of one missing word in a problem, the problem was thrown out, and no one received any points for it).
I asked my problem proofreader what he would do if I sent this problem to him to proofread. He assured me that he would throw it out. He also said:
"I think this is a wonderful problem for a class discussion, but not for any type of grade or for a competition. There is far too much ambiguity for it to be a problem with a well defined answer."
* Even the St. Ives problem is ambiguous; there isn't actually a solid reason to conclude that the man with seven wives is going in the opposite direction; the narrator could have simply caught up with the man (all things considered, he's probably going fairly slowly!) and struck up a conversation with him. That is an appropriate usage of the word "meet," and the St. Ives problem is therefore ambigious.
Martha asks, "In a straight line equation, why is the slope change in y over change in x, instead of change in x over change in y?"
That's a great question, Martha. One simple answer would be to just say, "because that's the way it is." But there are better answers than that. Let me give you one. Consider the equation for a line, when written in slope-intercept form. It is:
y = mx + b, and we say that m is Δy/Δx. If you're not familiar with the Greek letter delta used here (Δ), it simply means "the change in", so we would read that fraction as "the change in y over the change in x." So the equation now is:
y = (Δy/Δx)x + b.
Now that we've established that, let's talk about units. In real-world situations, the axes would both have units. For example, if the linear equation was part of a word problem about a car traveling from place to place, the horizontal axis might have a time unit, such as hours, and the vertical axis might have a distance unit like miles.
So now let's look at how those units would fit into our equation:
y is a vertical value, so its units would be miles.
Δy is a vertical change, so its units would also be miles.
Δx is a horizontal change, so its units would be hours.
x is a horizontal value, so its units would also be hours.
b represents the y-intercept (which is a y-value when x = 0) so it also has the vertical unit, miles.
Therefore, the equation, written only in terms of its units, would look like this:
miles = (miles/hour)hour + miles
Notice what happens when you multiply out (miles/hour)hour - you get just miles, leading to:
miles = miles + miles.
This is exactly what we need; when you add a two mileages, you get another mileage.
But consider what this would look like if m was Δx/Δy instead of the other way around. We would have:
miles = (hour/miles)hour + miles
miles = hour2/miles + miles, which is about the most absurd conglomeration of nonsensical units I've ever seen.
So that's one way of looking at the question, "Why is the slope Δy/Δx?" Because if it was the other way around, it would produce absurd results.
Sherry from Los Angeles asks, "I read that the method for subtracting without regrouping works all the time. But what about a problem like 6563 - 1998. You can take 1 away from each but still need to regroup. I’m a teacher and got so excited when I saw this, but it doesn’t always work??"

Hi Sherry, you're probably referencing this meme here. This meme shows subtracting a quantity from a number that has all zeroes after the first digit. Does this always work? Yes it does. Because if all the digits are zeroes, subtracting one from the number turns all the zeroes into nines, which means you don't ever have to regroup/borrow to finish the problem.
But that's only if those digits are all zeroes to begin with. What are the real world situations where this is likely to happen? If you're making change at a store. If you've paid with a 50 dollar bill, and the cost of the item is $24.32, your change would be $50.00 - 24.32. You can simplify this problem by rewriting it as $49.99 - 24.31 = $25.68.
Your question is, essentially, what if the first number doesn't end with all zeroes after the first digit?
And the answer is, it still works, but is not as likely to be practical. Here's an example: 1002 - 865. What we want to do is change the first quantity so it ends with nines. To do that, we subtract three instead of one. Which means, of course, that we have to subtract three from the second quantity as well: 999 - 862 = 137.
So now we get to your example: 6563 - 1998. We ask ourselves, what would we need to subtract from the first quantity to make it end in nines? Answer: 564. But that means we have to subtract 564 from the second quantity as well. In this particular case, we can do that subtraction without regrouping: 1998 - 564 = 1434. So 6563 - 1998 = 5999 - 1434 = 4565. But if regrouping had been required at the second step, we would have had to do our process again, and we'd end up with a cascading series of subtractions which would have been far more ugly than just regrouping in the first place.
As a general rule of thumb, even though it does (theoretically) work for problems like the one you suggested, in practice, it's very cumbersome, and I wouldn't recommend doing it that way.
"I just had an odd revelation in math today. I'm a seventh grader, and my teacher suggested I email a professor. We were doing some pretty basic math, comparing x to 3 and writing out how x could be greater, less than or equal to 3. But then it occurred to me; would that make a higher probability of x being less than 3? I mean, if we were comparing x to 0, there would be a 50% chance of getting a negative, and a 50% chance of being positive, correct? So, even though 3 in comparison to an infinite amount of negative and positive numbers is minuscule, it would tip the scales just a little, right?" ~ Ella from California
Good morning Ella,
This is a very interesting question! For the sake of exploring this idea, can we agree that we’re talking about just integers (In other words, our random pick of a number could be -7, or 8, but it can’t be 2.5 or 1/3)? You didn’t specify one way or the other, and limiting our choices to integers will make it simpler to reason it out.
I’d like to start by pointing out that doing a random selection from all integers is a physical impossibility in the real world. There are essentially three ways we could attempt it: mental, physical, and digital. All three methods are impossible to do.
Mental: Your brain is incapable of randomly selecting from an infinite (unbounded) set of integers. You’ll be far more likely to pick the number one thousand than (for example) any number with seven trillion digits.
Physical: Write integers on slips of paper and put them in a hat. Then draw one. You’ll be writing forever if you must have an infinite number of slips. You’ll never get around to drawing one!
Digital: As a computer programmer who develops games for this site, I often tell the computer to generate random numbers for me. It looks like this: number = rand(-10000, 10000), and it gives me a random integer between -10000 and +10000. But I can’t put infinity in there. Even if I could, it would require an infinite amount of storage to create infinitely large random numbers. (The same issue holds true for doing it mentally, by the way – your brain only has so much storage capacity!)
Okay, so having clarified that this is not a practical exercise, we have to treat it as purely theoretical. So let’s talk about theory. Mathematically, we define probability as follows:
Probability of event happening = (desired outcomes)/(possible outcomes).
For example, If I pull a card from a deck of cards, what’s the probability that it’s an Ace?
Probability of an Ace = 4/52, because there are 4 desired outcomes (four aces) out of 52 possible outcomes.
But here’s where we run into a problem. The definition of probability requires you to put actual numbers in. And infinity is not a number. I have hilarious conversations with my five-year-old son about this – someone told him about infinity, and he just can’t let go of the idea. "Daddy, infinity is the biggest number, but if you add one to it, you get something even bigger." Infinity can’t be a number, because you can always add one to any number, giving you an even bigger number, which would mean that infinity is actually not infinity, since there’s something even bigger.
So here’s where we’re at: we can’t do this practically, and we also can’t do it theoretically, using our definition of probability. So instead, we use a concept called a “limit” to produce our theoretical result. This may get a bit complicated for a seventh grader, so I'll forgive you if your eyes glaze over for the next couple paragraphs!
Let’s forget for a moment the idea of an infinite number of integers, and focus on integers in the range negative ten to positive ten. If we wanted the probability of picking a number less than 3, we’d have: Probability = 13/21, because there are 13 integers less than 3, and a total of 21 in all (ten negatives, ten positives, plus zero). What if the range was -100 to +100? Then Probability = 103/201. If the range was -1000 to +1000, we’d have 1003/2001.
Now let’s take this a step further and say that the integers range from -x to +x, where x is some integer we pick. The probability is (x + 3)/(2x + 1). Now we ask, “As x gets bigger and bigger, what does this fraction approach?” Mathematically, we write it as shown in the image below:
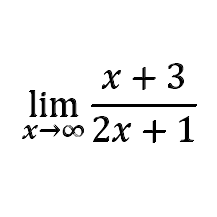
We'd read this as: "the limit as x approaches infinity of (x + 3) over (2x + 1)."
Evaluating limits like this is something my Pre-Calculus and Calculus students work on. Don’t worry, I’m not going to try to make you evaluate it – I’ll just send you here: Wolfram Limit Calculator. In the first textbox, type “inf” and in the second textbox, type (x + 3)/(2x + 1). Then click submit. The calculator will tell you that the limit is 1/2.
That’s probably not what you wanted to hear, right? You wanted me to tell you that the probability is just a tiny bit more than 1/2. And I sympathize with that – I’d like it to be more than 1/2 too! But remember that since infinity isn’t a number, we can’t plug it into our probability formula, so the probability doesn’t exist; only the limit of the probability exists. And that limit is 1/2.
Just for fun, if we could do arithmetic operations on infinity, I could solve it this way: “How many integers are there less than 3? An infinite number. How many integers are there three or greater? An infinite number. How many is that in all? Twice infinity. Therefore the probability is ∞/(2∞) = 1/2.” We can’t do arithmetic operations on infinity like that, because if we try, we eventually end up with some weird contradictions. But even so, it’s interesting that we end up with the same answer by reasoning it out that way!
PS - For clarification, "Professor Puzzler" is a pseudonym, and I'm not actually a professor. I'm a high school math teacher, tutor, and writer of competition math problems. So if your teacher needs you to contact an "actual professor," you should get a second opinion.
"I was told that when I'm rounding, if the number is less than 0.5, I round down, otherwise, I round up. But couldn't that mean more things rounding up than down, since 0.5 is right in the middle, and it gets rounded up?" ~ Quin from Chicago
Hi Quin, before I give you an answer, let me give an example of what you're talking about, to make sure all my readers understand your question.
Suppose you have 8 numbers: 4.1, 3.2, 2.5, 4.5, 5.5, 7.5, 1.6, and 4.9. There are just as many numbers with the tenths place below 0.5 as there are above 0.5, so you might expect that half of them round down, and half of them round up. But that's not what happens. Only two of them round down, and the other six found up. That seems very unbalanced.
Some people might wonder why that even matters. It matters if you have a lot of numbers and you're adding them together.
If you add all of the numbers above you get 33.8 But if you rounded them all, and then added them, you would end up with 36, which is a 6.5% error from the unrounded sum. Now, we don't expect the rounded sum to exactly match the unrounded sum, but this oddity that occurs when you have a bunch of numbers exactly at the midpoint of the rounding makes us wonder (as it made you wonder) if there might be a better way to do this.
It turns out there is an alternative method of rounding which is used in the circumstances described above:
- There are many numbers being added or averaged
- It's not unreasonable to expect that many of the data points will be exactly at the center mark 0.5
Under these circumstances, we can use the following rule for rounding:
If the decimal portion is less than 0.5, we round down, if the decimal portion is more than 0.5, we round up, and if the decimal portion is exactly 0.5, we look at the place value to the left of the five (yes, really, the left!). If it's an odd number, you round up, and if it's an even number, you round down.
For example, our four numbers above that end with a five would round as follows:
2.5 rounds to 2
4.5 rounds to 4
5.5 rounds to 6
7.5 rounds to 8
Another way of saying this is that we always round to the even number in the circumstance where the decimal is exactly 0.5.
So what happens if we do this? Our sum for the values given is 34, which is closer to the 33.8.
There's no guarantee that you won't end up with significant rounding discrepancy (if, by random chance, all your values were less than 0.5, your sum would be way off no matter how you round), but the odds of having large discrepancies decreases if you use this method.
The same method can be used at any place value. If you are rounding 135 to the nearest ten, it would be 140, but 125 would be 120.
Should you use this method of rounding? If you're a student, the answer is: only if your teacher tells you to do it this way!


