Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
This blog post is about the "Monty Hall Problem" - which you can find a blog post about here: Ask Professor Puzzler about the Monty Hall Problem, and a game simulation here: Monty Hall Simulation.
Larry from Louisiana writes: "Relating to the 3 door problem the answer given is just plain silly. Consider everything the same except you now have two players, one selects door one and the other selects door two. Now door three is shown to have a goat so, according to the given solution both players switch doors and each now has a 66% chance of winning? This may be possible in the new math but it is not in the old math that I learned."
Hi Larry, thanks for the message.
Before responding, I'd like to mention, in case anyone is confused by the "goat" part of your message, that in different versions of the game either two doors are empty, or they contain a donkey, or a goat, or some other silly prize. In the blog post here on this site I refer to the door as being empty, but to make my answer consistent with Larry's comment, I'll refer to the empty doors as containing a goat.
I'd also like to add that when I'm writing math problems for math competitions, my proofreader and I always comment - half joking (which means half serious!) that we hate probability problems, and wish we didn't have to write them. Probability problems can be very tricky, and it's easy to overlook assumptions we make that completely change our understanding of the problem.
In the case of the Monty Hall problem, there are a couple hidden assumptions that can be overlooked.
- Since the game show host always shows the contestant an empty door, that implies (even though this is not always stated outright) that he knows which door contains the prize. His choice is dependent on his own knowledge.
- Since only one door has been opened, the game show host has a choice, and it is always possible for him to choose an empty door.
It may be helpful to think of the game show host as a "player" or "participant" in the game. If the game show host cannot operate under the same conditions within the game, it is not the same game.
The game you proposed is an entirely different game with conditions that violate the conditions stated above. Specifically, even though in your stated scenario the game show host shows a goat, we need to understand that it is not always possible for him to choose a goat door; if the contestants have each picked a goat door, there is no door left for him to show except the one with the prize. In other words, the game show host's role is completely different. While he still knows which door contains the prize, he no longer has a choice, and (just as importantly) it is not always possible for him to choose an empty door. Another way of saying this: in your game, the host is no longer a participant in any meaningful way.
Since your game has conditions that violate the conditions of the Monty Hall Problem, it is not the same game, and we shouldn't expect it to have the same probability analysis. In fact, it doesn't, and you correctly observed that it wouldn't make sense for it to work out to the same probabilities.
I would encourage you to try out the simulation I linked at the top of this page; if you're willing to trust that I haven't either cheated or made a mistake in programming it, you'll see that the probability really does work out as described. And if you don't want to put your trust in my programming (which is fine - I think it's good for people to be skeptical about things they see online!), I'd encourage you to get a friend and run a live simulation. The setup looks like this:
- Take three cards from a deck, and treat one of them as the "prize" (maybe the Ace of Spades?)
- You (as the game show host) spread the three cards face down on the table. Before you do, though, remember that you're going to have to flip one of the cards that isn't the Ace of Spades, which means you need to know which card is the Ace of Spades. So before you put the cards on the table, look at them.
- Now ask your friend to pick one of the cards (but don't look at it).
- Since you know which card is the Ace of Spades, you know whether he has selected correctly. If he's selected correctly, you need to just randomly pick one of the other two cards to show him. If he hasn't picked the Ace of Spades, you know which one is the Ace of Spades, so you show him the other.
- Now ask him if he wants to switch. You'll need to agree beforehand whether he'll always switch or never switch, but he should be consistent and make the same choice each time.
- Do steps 2-5 about 100 times. If your friend always chooses to switch, you'll find that he wins about 2/3 of the time, while if he never switches, he'll win about 1/3 of the time.
I've had classes of high school math students break up into pairs and run this simulation, and the results always come out as described above. Happy simulating!
Sarah asks, "On your site you asked the following question and i believe your answer is incorrect. "I have a drawer with 10 socks. 6 are blue and 4 are red. I draw a blue sock randomly and then I draw a red sock randomly. Are these independent or dependent events". You answered even though it is without replacement these are independent. I believe the answer should be dependent, since there is one less sock in the draw when you pick the red one. Am I correct?"
Hi Sarah, thanks for asking this question. I went back and looked at the page your question refers to (Independent and Dependent Events) and realized that the question you were asking about may be a bit ambiguous in how it's worded. Does it mean:
- I drew a sock specifically from the set of blue socks (in other words, I looked in the drawer to find the blue socks, and then randomly selected from that subset) or...
- I reached into the drawer without looking, and randomly pulled out a sock from the entire set, and that randomly selected sock happened to be blue.
I write competition math problems for various math leagues, and I always hate writing probability problems, because they can be so easily written in an ambiguous way (my proofreader hates proofreading them for the same reason). In this case, let's take a look at these two possible interpretations of the problem.
In the first case, the two events are clearly independent; it doesn't matter which of the blue socks was chosen; there are still 4 red socks, and the probability of choosing any particular red sock is 1/4. Thus, the second event is not affected by the first event.
In the second case, I randomly pulled a sock from the drawer, but now we're given the additional information that this sock happened to be blue. So this means that when I reach back into the drawer, there are now nine socks to choose from (not four, as in the previous case, because we assume I'm picking from the entire contents of the drawer.) Since we know that the sock I first chose is blue, there are still 4 red socks, so the probability of choosing a red is 4/9. We get a different answer if we read it this way, but we still have two events that don't affect each other. Since we know the first sock was blue, it doesn't matter which blue sock it was. The specifics of the draw don't affect the outcome of the second draw.
Here's how to make these two events dependent: don't specify that the first draw was blue. Now the result of the second draw is very much dependent on whether or not the first draw was blue. That's probably the situation you were thinking of.
Thank you for asking the question - as a result of your question, I'm going to do some tweaking in the wording of that problem. I don't want it to be ambiguous - especially since the second reading of the problem delves into conditional probabilities, which I don't address on that page!
"I just had an odd revelation in math today. I'm a seventh grader, and my teacher suggested I email a professor. We were doing some pretty basic math, comparing x to 3 and writing out how x could be greater, less than or equal to 3. But then it occurred to me; would that make a higher probability of x being less than 3? I mean, if we were comparing x to 0, there would be a 50% chance of getting a negative, and a 50% chance of being positive, correct? So, even though 3 in comparison to an infinite amount of negative and positive numbers is minuscule, it would tip the scales just a little, right?" ~ Ella from California
Good morning Ella,
This is a very interesting question! For the sake of exploring this idea, can we agree that we’re talking about just integers (In other words, our random pick of a number could be -7, or 8, but it can’t be 2.5 or 1/3)? You didn’t specify one way or the other, and limiting our choices to integers will make it simpler to reason it out.
I’d like to start by pointing out that doing a random selection from all integers is a physical impossibility in the real world. There are essentially three ways we could attempt it: mental, physical, and digital. All three methods are impossible to do.
Mental: Your brain is incapable of randomly selecting from an infinite (unbounded) set of integers. You’ll be far more likely to pick the number one thousand than (for example) any number with seven trillion digits.
Physical: Write integers on slips of paper and put them in a hat. Then draw one. You’ll be writing forever if you must have an infinite number of slips. You’ll never get around to drawing one!
Digital: As a computer programmer who develops games for this site, I often tell the computer to generate random numbers for me. It looks like this: number = rand(-10000, 10000), and it gives me a random integer between -10000 and +10000. But I can’t put infinity in there. Even if I could, it would require an infinite amount of storage to create infinitely large random numbers. (The same issue holds true for doing it mentally, by the way – your brain only has so much storage capacity!)
Okay, so having clarified that this is not a practical exercise, we have to treat it as purely theoretical. So let’s talk about theory. Mathematically, we define probability as follows:
Probability of event happening = (desired outcomes)/(possible outcomes).
For example, If I pull a card from a deck of cards, what’s the probability that it’s an Ace?
Probability of an Ace = 4/52, because there are 4 desired outcomes (four aces) out of 52 possible outcomes.
But here’s where we run into a problem. The definition of probability requires you to put actual numbers in. And infinity is not a number. I have hilarious conversations with my five-year-old son about this – someone told him about infinity, and he just can’t let go of the idea. "Daddy, infinity is the biggest number, but if you add one to it, you get something even bigger." Infinity can’t be a number, because you can always add one to any number, giving you an even bigger number, which would mean that infinity is actually not infinity, since there’s something even bigger.
So here’s where we’re at: we can’t do this practically, and we also can’t do it theoretically, using our definition of probability. So instead, we use a concept called a “limit” to produce our theoretical result. This may get a bit complicated for a seventh grader, so I'll forgive you if your eyes glaze over for the next couple paragraphs!
Let’s forget for a moment the idea of an infinite number of integers, and focus on integers in the range negative ten to positive ten. If we wanted the probability of picking a number less than 3, we’d have: Probability = 13/21, because there are 13 integers less than 3, and a total of 21 in all (ten negatives, ten positives, plus zero). What if the range was -100 to +100? Then Probability = 103/201. If the range was -1000 to +1000, we’d have 1003/2001.
Now let’s take this a step further and say that the integers range from -x to +x, where x is some integer we pick. The probability is (x + 3)/(2x + 1). Now we ask, “As x gets bigger and bigger, what does this fraction approach?” Mathematically, we write it as shown in the image below:
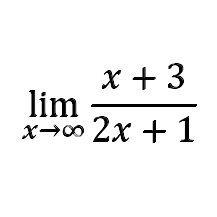
We'd read this as: "the limit as x approaches infinity of (x + 3) over (2x + 1)."
Evaluating limits like this is something my Pre-Calculus and Calculus students work on. Don’t worry, I’m not going to try to make you evaluate it – I’ll just send you here: Wolfram Limit Calculator. In the first textbox, type “inf” and in the second textbox, type (x + 3)/(2x + 1). Then click submit. The calculator will tell you that the limit is 1/2.
That’s probably not what you wanted to hear, right? You wanted me to tell you that the probability is just a tiny bit more than 1/2. And I sympathize with that – I’d like it to be more than 1/2 too! But remember that since infinity isn’t a number, we can’t plug it into our probability formula, so the probability doesn’t exist; only the limit of the probability exists. And that limit is 1/2.
Just for fun, if we could do arithmetic operations on infinity, I could solve it this way: “How many integers are there less than 3? An infinite number. How many integers are there three or greater? An infinite number. How many is that in all? Twice infinity. Therefore the probability is ∞/(2∞) = 1/2.” We can’t do arithmetic operations on infinity like that, because if we try, we eventually end up with some weird contradictions. But even so, it’s interesting that we end up with the same answer by reasoning it out that way!
PS - For clarification, "Professor Puzzler" is a pseudonym, and I'm not actually a professor. I'm a high school math teacher, tutor, and writer of competition math problems. So if your teacher needs you to contact an "actual professor," you should get a second opinion.

This morning's question is, in essence, if you know the probability of an event happening, what is the probability of it NOT happening?
To answer this question, it's good to remember that a probability is a ratio. It is: [number of desired outcomes] : [total number of outcomes] (assuming that all outcomes are equally likely).
Let's consider the flipping of a coin. Suppose you want the probability of getting heads. The number of desired outcomes is 1. The total number of outcomes is 2.*
'So the probability is 1/2. So what is the probability of NOT getting heads? Well, that's the same as the probability of getting tails. Desired outcomes: 1, possible outcomes 2. Thus, the probability is also 1/2.
* I've had students argue that a coin could land on its rim, so there are actually 3 possible outcomes. I point out to them that there are a couple problems with that. First, if it lands on the rim, we re-roll the coin, so that really doesn't count. Second, if we decided to keep that roll, we can't use our ratio definition above, because all outcomes are not equally likely.
So now let's switch gears and talk about a six-sided die. What is the probability of getting a perfect square when you roll the die? Well, there are 2 perfect squares that are possible results: 1, and 4. So desired outcomes = 2, total outcomes = 6. Thus the probability is 2/6 (we can simplify that to 1/3, but for now I'd like to keep in the form 2/6).
What is the probability of NOT getting a perfect square? Well, there are 4 numbers that aren't perfect squares: 2, 3, 5, and 6. Desired outcomes = 4, total outcomes = 6. Probability is 4/6.
Let's try one more example. What is the probability of rolling a total of 12 if you roll two six-sided dice?
There is only one way to get a sum of 12: you need a six on each die. There is a total of 6 x 6 = 36 possible outcomes. Desired = 1, Total = 36, probability = 1/36. What about the probability of NOT rolling a 12? Well, you could list off all the possible outcomes, but let's reason this out instead. If there are 36 possible outcomes, and only one of them leads to a sum of 12, how many don't lead to a sum of 12? The answer should be fairly obvious: 36 - 1 = 35. Desired = 35, total = 36, probablity = 35/36.
Now let's put those results together:
Coin: 1/2; 1/2
Die: 2/6; 4/6
2 Dice: 1/36; 35/36
Hopefully you can see a pattern here: in each case, the probabilities add to 1. And, if you think about how we reasoned out the example with two dice, that should make sense to you; every outcome is either a desired or a not desired outcome. There are no other options. So when you add together those options, you get the total number of outcomes. And [total outcomes]/[total outcomes] = 1.
We can write this rule as an equation like this: P(x) + P(~x) = 1.
In words: The probability of x, plus the probability of NOT x equals 1.
I hope that helps!
Yesterday, I answered a question about the Monty Hall Three-Door Game, which you can read about in the previous blog post. After posting the article, I shared it on social media, and commented that talking about this problem feels like wading into a murky swamp, because everyone brings their own assumptions into the problem, and it's tough to guess what those assumptions are.
But I realized, too, that it's not just this problem; it's probability in general. I love probability, and I hate probability. Whenever a district/county/state asks me to write competition math problems for their league or math meet, I know that I need to give some probability problems - everyone expects it! But there's no kind of math problem that I'm more afraid that I'll mess up. I'm grateful for a proofreader to give my problems a second pair of eyes (although my proofreader shares my feelings about probability). More often than not, I'll figure out a way to write a program to function as an electronic simulation of my problem, to verify empirically that I have arrived at the right solution.
Anyway, one of the reasons that probability feels so murky to me is that gut reactions can lead you astray. The Three-Door game is a prime example of how those gut reactions can mess you up. Monty asks you to pick a door, knowing that one of those doors has a prize behind it, and the other two have nothing. After you pick, Monty opens one of the other doors to show you that it's empty, and asks you if you'd like to keep your original guess, or switch to the other unopened door.
Most people's gut reaction is that it doesn't matter whether you keep your original guess or switch to a different guess. This gut reaction is wrong, as you can verify by playing the simulation I built here: The Monty Hall Simulation. For those who are still struggling with this, I'd like to offer a couple different ways of looking at the problem.
The "Not" Probability
We tend to focus on the probability of guessing correctly the first time. Instead, let's focus on the probability of NOT guessing correctly. If you picked door A, then the probability that you were correct is 1/3. This means that the probability you did not guess correctly is 2/3. But really, what is that? It's the probability that either door B or door C is correct.
So if PB is the probability that door B holds the prize, and PC is the probability for door C, we can write the following equation:
PB + PC = 2/3.
Now Monty opens one of those two doors (we'll say C), that he knows is empty. This action tells you absolutely nothing about the door you opened, but it does tell you something about door C - it tells you that PC = 0.
Since PB + PC = 2/3, and PC = 0, we can conclude that PB = 2/3. This is exactly the result which the simulation linked above gives.
Two Doors vs. One Door Choice
Related to the above way of looking at it, try looking at it with a set of slightly modified rules:
- You pick a door
- Monty says to you: "I'll let you keep your guess, or I'll let you switch your guess to both of the other two doors."
Under these circumstances, of course you're going to switch. Why? Because if you keep your guess, you only have one door, but the choice Monty is offering you is to have two doors, so your probability of winning is twice as great. In a sense, that's actually what you're doing in the real game, even though it doesn't appear that way. You're choosing two doors over one, and the fact that Monty knows which one of those two doors is empty (and can even show you that one is empty) doesn't change the fact that you're better off having two doors than one.

