The "Distance from the Hurricane" problem is one I did with my upper-level math classes, just after receiving an inquiry from someone in Florida who had a question about Hurricane Irma. Even though hurricanes are more science than math, we spent some time talking about hurricanes in general, and the specifics of the current hurricanes developing across the Atlantic. I think it's good to make sure students are aware of, and sense the gravity of, natural disasters like this.

The problem is an excellent one to work through with students. I did this problem on the white board, taking input from the students on what to do next. This problem contains the following features:

• Requires the ability to convert a real-world scenario into a geometric diagram
• Requires the ability to recognize that the problem cannot be solved without additional information
• Requires the ability to understand the diagram well enough to insert extra line segments with real-world meaning
• Requires the ability to identify places where additional segments could be inserted to create useful triangles
• Requires both trigonometry and geometry skills to solve

The problem can be solved in multiple ways. I let the students steer the direction we take, but when we are finished, I show them alternate methods they can use to finish solving the problem.

The problem is provided (without any diagrams) in the slide show above, and can be projected on a screen for your students. The text of the problem is also given below.

A circular hurricane has a diameter of 400 miles. It is traveling at a speed of 20 mph. A house is 600 miles away from the eye of the hurricane. How long will it be before the house is under the hurricane?

The tendency of most students is to use the basic d = rt formula to solve this problem as follows:

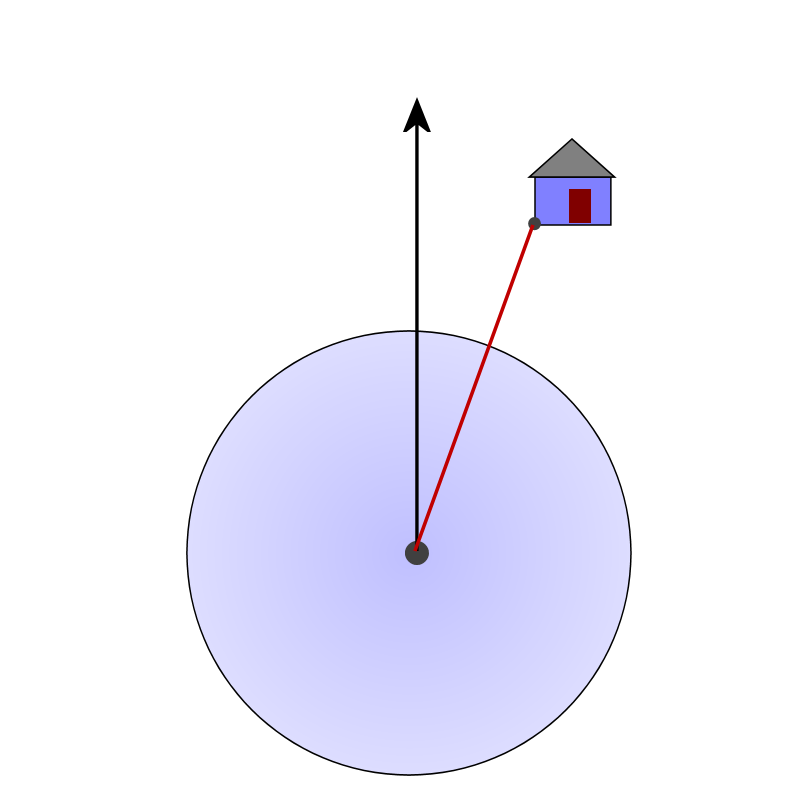
d = 600 - = 400; t = = = 20 hours

This is not a complete solution, as it assumes that the hurricane is headed directly toward the house, when, in fact, the line connecting the eye of the storm to the house probably is not representative of the direction of the storm. In other words, the storm may be on track for the eye to pass by at a certain distance from the house, instead of going directly over it.

At this point I simply tell the students that their answer is not correct, but I don't identify the problem with their thinking. Depending on the class I might need to give them a hint. I might say something like, "Does the problem say what direction the hurricane is going?" or "I see you've drawn the hurricane eye passing over the house; does the problem say that's going to happen?"

After pondering this for a bit, students will hopefully recognize that a new diagram is required. The new diagram is provided below, and as a slide in the slide show.

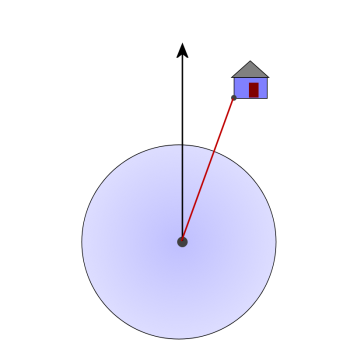
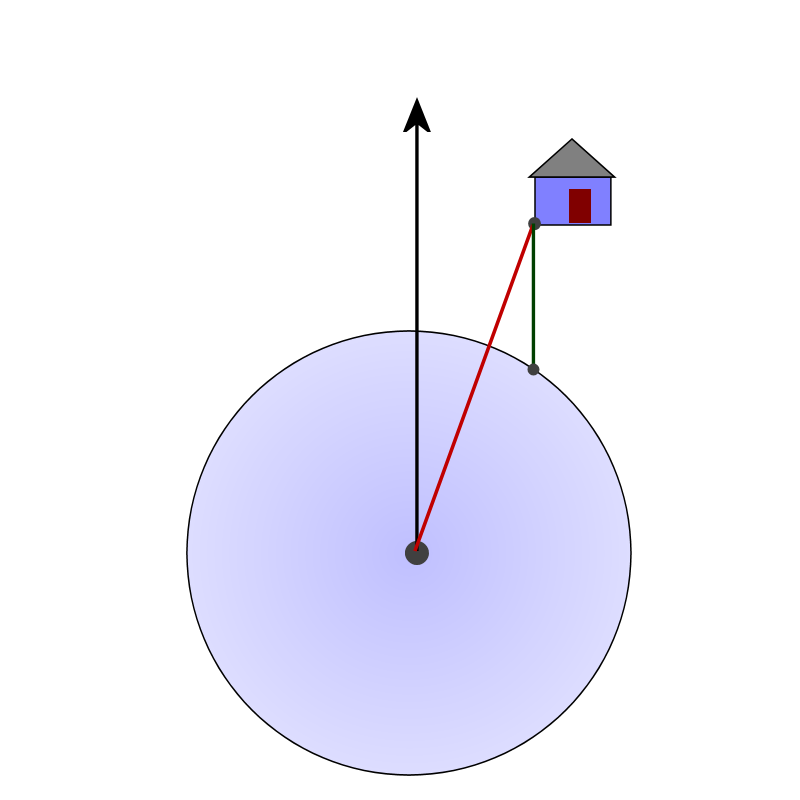
Once the students have a diagram similar to this one, you may need to direct their attention to the fact that there is no segment in the diagram that represents the distance they are looking for; the distance from the edge of hurricane to the house, in the direction of the hurricane's motion.

Additionally, students may have a hard time visualizing where this segment should go. If that's the case, you can encourage them to reverse their thinking and imagine that instead of the hurricane moving, and the house being stationary, the hurricane is stationary, and the house is moving toward the hurricane. This alternate visualization may help students recognize the segment they need, as shown in the slides, and below.

By now, students should have realized that this problem is unsolvable without knowing an additional piece of information. At this point I tell them that the angle between the motion of the hurricane and the red segment is 5 degrees. You could also label the angle Θ, and require students to carry the variable through, in order to obtain a formula in terms of Θ.

As an alternate approach, instead of telling the students the angle, you could tell them the distance of the eye's closest approach to the house (this would be represented by a horizontal segment connecting the house to the direction line of the hurricane). Although I haven't worked this approach through fully, I'm pretty sure it makes trigonometry unnecessary. Be sure to work out the details for yourself before you try it that way.

Now students need to draw in line segments to create triangles they can solve. Students will suggest a variety of line segments. I encourage them to come to the board and draw the segments themselves. Then we analyze the triangles they have created to determine whether the triangle adds any useful information, or allows them to find additional information. Often we will decide that the segments they add don't help, and we end up erasing them.

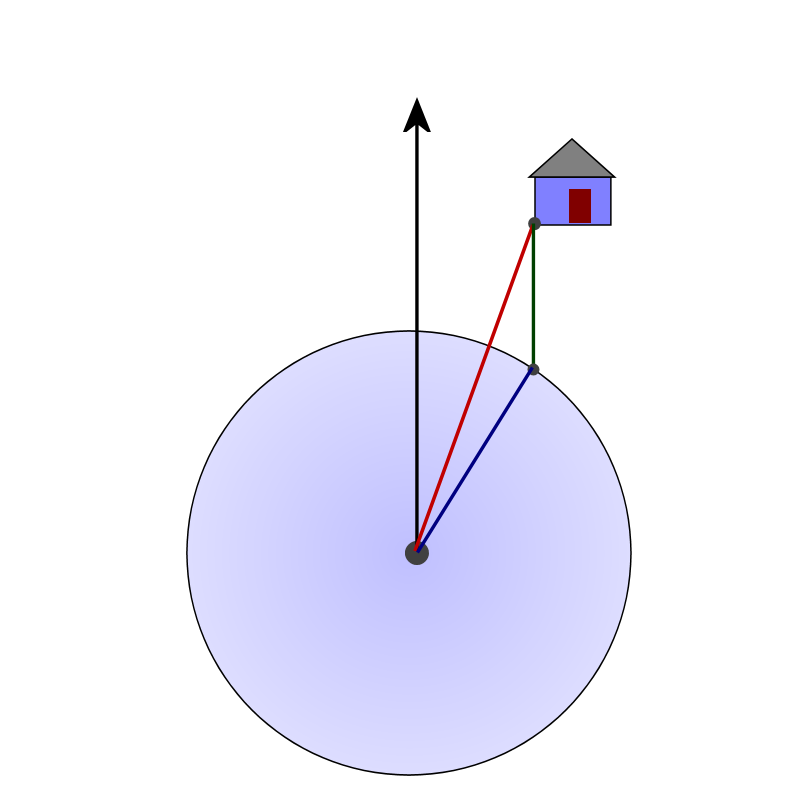
The diagram below shows one additional line segment, drawn from the eye of the storm to the intersection point of the house with the edge of the storm.

Students should identify that the blue line is the radius of the hurricane (200 miles) and the red line is the total distance (600 miles). Also, students should recognize that we have a pair of alternate interior angles (the hurricane's direction line and the green line are parallel) so the angle formed by the red and green lines is also 5 degrees.

At this point, some students may recognize that the triangle can be solved using the law of cosines. This is a cumbersome method, as it results in a rather ugly quadratic (and if you are carrying a Θ through the problem, it's even uglier). Nevertheless, if students want to go this route, they should be encouraged to do so. If they don't, this method should be pointed out when the problem is finished.

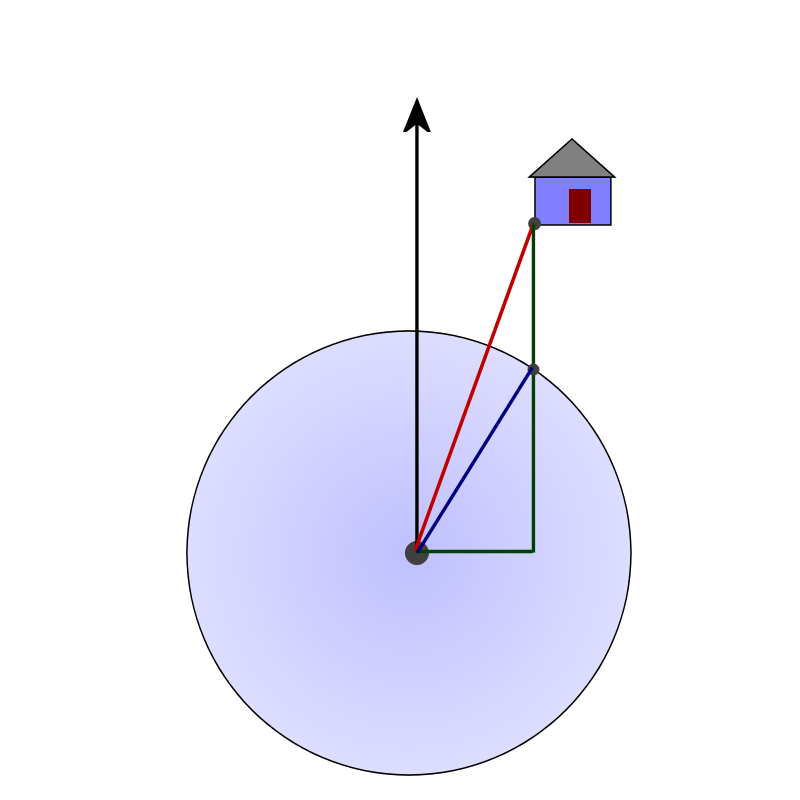
The other route that is helpful to take is to extend the green line segment and draw a perpendicular toward the eye. This is shown in the slide show, and below.

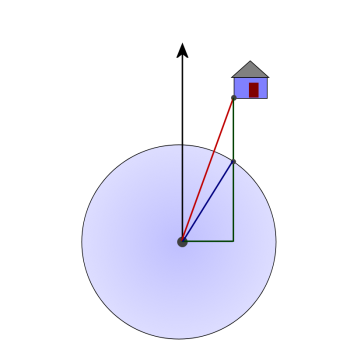
Since students know the length of the red segment, and the angle at the eye, they can use trigonometry to find the lengths of the legs of the right triangle which has the red segment as its hypotenuse.

Vertical = 600cos(5) = 597.7 miles
Horizontal = 600sin(5) = 52.3 miles

Similarly, they know that the blue hypotenuse is the radius of the hurricane, and they now know one of the legs of that right triangle, so they can use the Pythagorean Theorem to find the length of the lower portion of the green segment.

Vertical = = 193 miles

Subtracting this from the full length of the green segment gives the upper portion of the green segment, which is the distance required.

Hurricane distance = 597.7 - 193 = 404.7 miles

Finally, we can use the given hurricane speed to calculate the time until the storm reaches the house: 

t = = 20.2 hours

Again, different approaches can be taken to arrive at the solution, and students should not be "stifled" from trying different approaches, even if you know your approach is quicker. I try to make a habit of letting the students work out an approach, and if I know another approach that might work better, to show it to them when they're done. This takes more time, but also encourages students to look at problems from multiple perspectives.

From a science perspective, the diagram of this problem is very helpful in getting students to understand that the damage done to home and property has a significant relationship to the manner in which the hurricane approaches; if the eye passes a significant distance from the house, the house will pass through the outer (weaker) portions of the hurricane.

I read one blogger comment that the categories are meaningless, because they once went through a CAT 1 hurricane that did far more damage than a CAT 3 they had endured a couple years earlier. The category of the hurricane is not the only factor in play; going through the center of a CAT 1 hurricane is going to be more damaging than going through the edges of a CAT 3 hurricane.