Introduction

So far in our study of motion we have considered only motion along a straight line.  Now that we have been introduced to vectors, it is time to examine several kinds of motion in curved lines.  There are several kinds of curved line motion which occur commonly in nature which are simple enough for a beginning high school physics class to study.  First we will examine the motion of a projectile such as batted ball or a cannon ball.  The second type of curved line motion we will examine is the motion of an object in a circular path at a constant speed.  Closely related to this is the motion of a satellite.  The third type of motion is not truly motion in a curved line but is so closely related that it will be studied here.  It is a particular kind of back and forth motion called simple harmonic motion.  Each will be described in turn and sample problems will be solved for each kind of motion.

Projectile Motion

When an object is projected into space (thrown, batted or shot) in such a way that it moves up and down under the influence of gravity at the same time it moves horizontally, we call the motion projectile motion.  The path that the object follows is called its  trajectory.  In solving projectile motion problems we will assume that the object is moving slowly enough for us to neglect air friction and Iisnear enough to the surface of the earth for us to consider the acceleration of gravity to be a constant.

Before going any further review the sections in chapter 1 where an object is moving vertically up and down under the influence of gravity and the related problems . Be sure you can break a vector into components.  Review any sections and problems in chapter 3 that relate to this.  If you are having major difficulties with this old material you will have a great deal of difficulty with projectile motion.

To simplify the motion of an object moving in a trajectory we will break its motion up into two motions, vertical and horizontal.  These motions can then be considered more or less independently or each other.  The vertical motion is a uniformly accelerated motion with a downward motion of 9.8 .  The horizontal motion is a motion at constant speed.

Read the problem carefully and determine the initial conditions.  If the object has an initial motion which is neither horizontal nor vertical the first step is to determine the horizontal and vertical components of the initial velocity.  Make a list giving all known conditions and any quantity desired for both vertical and horizontal motion.  This will require two separate lists much as for the two object problems studied in chapter 1.  Some of the variables for the vertical and horizontal motion will be related.  For example, the time that the object will be in its trajectory is the same for both  vertical and horizontal components of its motion.  Express any unknown quantities as variables.

Use the equations for uniformly accelerated motion from chapter 1, equations 1 through 6, to find the value of any unknown quantity.  It may be necessary to solve a system of equations to determine the unknown quantities.

Sample Problem #1

A boy standing on the roof of Oxford Hills High School, 8m above the lawn, throws a ball horizontally at a speed of 25.  Determine how far from the building the ball will land and its velocity when it reaches the ground.

Sample Solution #1

Use equation 6 from chapter 1 on the vertical motion to determine the time the object was in the air.

Therefore Δt = 1.28sec

Now use this time and the information for the horizontal motion to find the horizontal distance moved.

To find the final velocity we need both the final vertical and horizontal components of the velocity.  The final horizontal component is the same as the initial horizontal velocity, 25 , since the horizontal motion has no acceleration.  To find the final vertical velocity:

Now sketch a vector diagram showing the vertical and horizontal components of the final velocity.
 

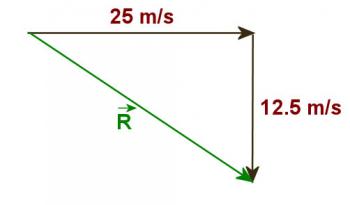
^{Figure 4.1.1}

Use the Pythagorean theorem to determine the resultant velocity and trig to determine the angle that the final velocity makes with the horizontal.

Sample Problem #2

A ball is thrown upward at an angle of 25º and a speed of 30 .  Calculate where the ball will strike the ground. 

Sample Solution #2

Before making up the table of given quantities it is necessary to determine the vertical and horizontal components of the initial velocity.  The vertical component will be equal to 30sin(25º) which is 12.7 and the horizontal component will be 30cos(25º) = 27.2 .  Now list all known and desired quantities in a table as done in problem 4‑1.  Fill in a variable for any unknown quantity.

     

Since the ball returns to the same level we have set the final vertical displacement equal to zero.  We have also made use of the fact that a ball thrown vertically upward will return to its original level with a speed equal to the negative of the speed with which it was thrown.

Use the known quantities for the vertical motion to calculate the time that the ball is in the air.

Use this time to calculate the horizontal distance traveled.

Sample Problem #3

A baseball player hits the ball toward the outfield wall.  The ball hits the bat at a height of 3 ft above the ground and leaves the bat at an angle of 40º above the horizontal with a speed of 150 .  It travels toward a wall which is 350 ft away and is 25 ft tall.  Determine if the ball will clear the wall.

Sample Solution #3

Before making up a table of initial and final conditions we need to decide how we are going to tell if the ball is a home run.  There are at least two ways. We could take the final point of the problem as the time when the ball has reached the wall and see how high it is then or we could take the final point as the time when the ball has reached vertical height of 25ft and see how far it has traveled at that point.  We will do it the second way.

We now need to calculate the vertical and horizontal components of the initial velocity.  By now you should be able to show that the initial vertical component is 150sin(40º) = 96.4 and the horizontal component is 150cos(40º) = 114.9 .  Now set up the table of known and desired quantities.

Note that the vertical distance is 22 ft not 25 ft.  This is because the ball started at a height of 3ft above the ground.  Now use the know quantities for the vertical motion to find when the ball is 22ft above the point of contact with the bat.

Note that since we have a quadratic equation there are two roots.  When you think about the problem you will see why.  The ball will actually be at the desired height twice, once on the way up and a second time on the way down. The time that concerns us, of course, is the time when the ball reaches the height of the wall on the way down*.  Now use that time and the horizontal component of the speed to find the horizontal distance traveled.

The ball does not return to the height of the wall until long after it has passed over the wall, therefore it is a home run.

To see if you understand the procedure, demonstrate that the ball will clear the wall by a distance of about 122ft.  Use the other approach mentioned at the start of the problem and find the height of the ball when it has traveled a horizontal distance of 350ft.         

One further comment is in order before going on.  Whenever a quadratic equation is solved it is possible that there is no real root.  What would have been the physical significance of imaginary roots for the quadratic equation in Δt?  This would have indicated that the ball would never have reached the height of the wall so you would have known that it was not a home run without going any further.

* In solving this problem using the method described, we've made the assumption that the ball is descending by the time it reaches the wall. A line drive of sufficiently high speed might hit the wall while still ascending. If this were the case, the two Δt values would represent the range of times in which the ball would have been high enough to clear the wall - if it hadn't crashed into it first. However, we understand that a 40 degree angle of inclination is not a line drive, and are therefore confident that the second Δt value is the one we want. To verify the assumption, find the horizontal distance at each value of Δt and show that 350 ft lies between the two values.

1.

A projectile is fired with a speed of 300ft/sec at an angle of 37 degrees with the horizontal. Compute the speed when it first reaches a height of 400ft.

2.

A golf ball is projected upward with a speed of 65m/sec at an angle of 45 degrees with the horizontal. What is its initial vertical velocity? What is its vertical velocity after 2.0sec? What is its horizontal velocity after 2sec? When the ball is descending, it strikes a building at a point 20m above the ground. What is the vertical component of the velocity at the instant the ball strikes?

3.

A gun is aimed at an angle of 30 degrees above the plain. The shell rises 600ft above the plain. How far will the shell travel horizontally? What is its velocity (magnitude and direction) 4.0sec after it is fired?

4.

A baseball player throws a baseball in from the outfield. As it leaves the player's hand, the ball makes an angle of 60 degrees with the horizontal. After 2.0sec the ball is still rising, but in a direction 30 degrees above the horizontal. Compute the speed of the ball in m/sec when released by the player.

5.

A ball is thrown at an angle of 60 degrees above the horizontal with a speed of 30m/sec. How high will it rise? What is the range? Where will the ball be at the end of 6 sec?

6.

A baseball rolls down a roof which makes an angle of 37 degrees with the horizontal. When the ball reaches the lower edge of the roof its speed is 30ft/sec. If this edge of the roof is 20ft above the level ground, at what horizontal distance from the edge will the ball strike the ground?

7.

A punted football traveled 64yd horizontally and stayed in the air 6.0sec. How high did it rise? What was the vertical component of the ball's initial velocity? What was the horizontal component of the ball's initial velocity? With what velocity did the ball leave the kickers foot?

8.

A workman sitting on the top of a roof of a house eating his lunch drops an orange. The roof is smooth and slopes at an angle of 30 degrees to the horizontal. It is 32ft long and its lowest point is 32 ft from the ground. How far from the house wall is the orange when it hits the ground?

9.

A person can throw a ball 40m on the earth. How far can he throw the ball on the moon if he throws it with the same speed? The acceleration of gravity on the moon is 1/6 that of the earth. (Assume that the ball is thrown horizontally in both cases)