You've seen the videos, you've probably shared them on Facebook or other social media...the videos that tell you, "This is how the Japanese multiply numbers!"

Except...do they really?

First, here's an example: 

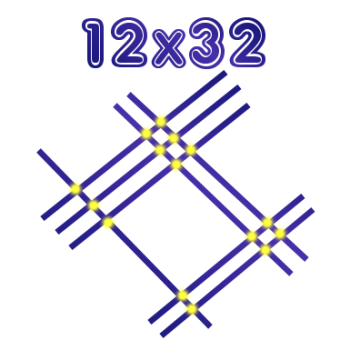
The question is, how do you multiply 12 x 32 the Japanese way?

Well, supposedly, the Japanese solve this by drawing one line diagonally from the left down to the right, followed by a pair of lines going in the same direction. The one line, followed by the two lines, represents the number 12.

Similarly, three lines are drawn together from the left up to the right, followed by two more lines from the left up to the right; these sets of lines (3 and 2) represent the number 32.

Now you draw a circle around every intersection point, starting over on the right. There are 4 intersection points. That means that the last digit is 4. In the middle there are six intersection points (at the top) and two more at the bottom, making a total of 8. Thus, the middle digit is 8. Finally, there are 3 intersection points on the left, so the first digit is 3.

Therefore, the answer is 384.

I'll give you a second to use your old algorithm (or your calculator!) to verify that this is correct.

Does this always work?  Well, yes...and no.

The videos that display this process rarely show what happens if the sum of your intersection points is greater than 10. If that happens (which, really, why wouldn't it?) your process is a bit more cumbersome, and you have to transport a group of ten dots as a single dot in the next place value. In other words, you have to carry.

That's not a big deal, though; you already have to carry with your algorithm. So what's the problem with this algorithm? Well, the people who make these videos are very careful to make sure they do multiplications with small digits. You'll see things like 12 x 32, or 113 x 21, but you'll never see one of these videos with 978 x 88.

Why not? Gee...I don't know...why don't you try drawing the diagram for that problem, and see what it looks like. While you're busy drawing that diagram, I'll solve about five more multiplication problems. You'll need to draw forty lines, circle and count 201 intersection points, and meanwhile, I've moved on to my division lesson, because I got tired of waiting for you.

Do the Japanese do this when they're multiplying? Of COURSE NOT! I don't know if any Japanese teachers actually show this to their students (read comments on videos and you'll find people saying things like, "I taught math in Japan for 25 years and never saw this.") but if they do show it to their students, it's only as a way of visualizing place value in a different way; nobody actually expects their students to use this as their go-to multiplication algorithm.

And yet, wherever you see videos like this, you'll see comments from parents saying things like, "If I had learned it this way, I wouldn't have ever had problem with math," or "I'm going to meet with my kid's teacher and ask why in the world she's not teaching it this way!"

Oh dear! Please give your child's teacher a break! Let them teach math, and don't force them to spend an afternoon explaining to you why the latest craze to hit the internet isn't actually even slightly useful as a multiplication algorithm.

And if you got fooled by the "Japanese Multiplication" video, odds are good you also got fooled by the "Oh noes! Have you seen how Common Core does subtraction????" videos, so you'll want to read our post about "Common Core" Subtraction.