Leap year! What is it good for? Absolutely nothing? Or does it actually serve a purpose?

Okay, let me explain how this question came about... 

Today our little girl turned one year old. She was born at 1:09 in the afternoon on February 11^th, 2015. I mentioned this to my Algebra students today, and then added that at about 7:09 this evening, she will have completed one entire revolution around the sun.

They looked at me like I had a third eye growing out of the middle of my forehead (okay, they often look at me that way...). "If she was born at 1:09 in the afternoon, isn't that when she's finished her first revolution around the sun?"

Nope! You see, a year is not exactly 365 days long. A year (the amount of time it takes for the earth to travel once around the sun) is actually a little bit longer than 365 days. It's right around 365.25 days. So our little girl finished her first trip around the sun a quarter of a day after her birth hour. Since a quarter of a day is 6 hours (²⁴/₄ = 6), and 7:09 is six hours after 1:09, it was this evening that she finished her first trip around the sun.

This led the class into a discussion of leap year, because that quarter of a day is the reason why leap years exist. If our calendar year is a quarter of a day shorter than a solar year (a solar year is the time it takes earth to travel once around the sun), then every four years, we'll end up with an extra day that needs to be stuffed into the calendar somewhere. So we decided to make that day be February 29^th. It was actually very good thinking - since February was by far the shortest month, putting that extra day in the calendar in February helps to even out the months a little*.

"Of course," I added, "It's not exactly that simple, because a solar year is not exactly 365.25 calendar days. It's just a little bit less than that. Which is why, every hundred years, we skip a leap year."

"WHAT?"

"Oh yes. If the year number is divisible by 100, we don't have a leap year."

"Really?"

"Sure. Unless, of course, the year is also divisible by 400. In that case, we do have leap year."

It was at this point that one of my students suggested that Leap Year might be good for absolutely nothing. Actually, what she said was, "I don't see why we need to do all this math. Why can't we just forget leap year?"

Ah. Good question. Let me try to explain it to you. Take a look at the picture below. In it you'll see the sun, and planet earth. Earth is following that almost-circular orbit around the sun, and I've marked the position of the earth with the time: the time of my little girl's birth.

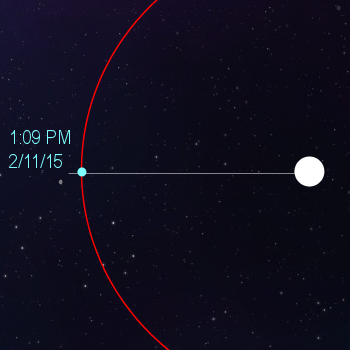
When the earth is in this position, we are essentially in the dead of winter.

Now, where will the earth be 365 days after this point in time? I'll show you. In the picture below I've marked 1:09 PM on Feb 11, 2016. That's the second line I've drawn. "That's it?" you might think. "Why that's hardly any difference at all!"

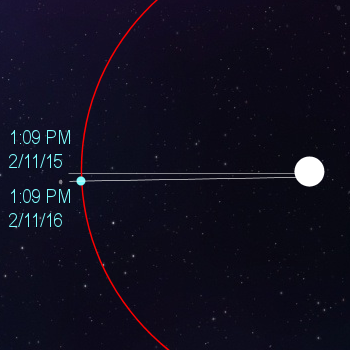
Sure, that's true. But that tiny little difference (about a quarter of a degree every year) will add up as the years pass.

Suppose we stop having leap years. And suppose that my little girl lives to be 120 years old (hey, who knows what scientific advances will happen in her lifetime?). When she's 120 years old, all those quarter days will have added up to an entire month. She'll be celebrating Christmas on December 25th, but the weather will be like Thanksgiving weather instead of Christmas weather, because the calendar year will have shifted an entire month from the solar year - and it's the solar year that determines our seasons, regardless of what we declare them to be on our calendar!

Can you imagine? She'll say to her great-grand kids, "I remember when we used to have blizzards on Christmas..." and they'll say, "That's silly, gram! We never have snow like that in December!"

And then, if we keep on like this, all those quarter-days will add up to 2 months, then 3. Eventually, our calendar year will be completely backwards from the solar year. Students will have June, July, and August off from school, and it will be snowing and bitter cold all through "summer" vacation. Then they'll be going to school all through the wonderfully warm and sunny beach weather of December, January, and February.

"Okay," my student said, "We can keep leap year."

I thought you might feel that way.

* Professor Puzzler's father, commonly known around here as "Mr. Physics," adds the following leap-year trivia:

"There is another reason whey they choose February for the extra day. Remember, under the Julian calendar the year started at March; February was the last month of the year. That is why September (7), October (8), November (9) and December (10) are numbered wrong.

"Another interesting bit of trivia. When Caesar Augustus decided that he needed a month named for him (August) he realized that to show himself equal to his Great Uncle Julius he needed to have 31 days in August so he stole a day from February leaving it with only 28 days."