Twelfth grader Jodi asks, "Hi Professor, if you could help me understand this problem I would highly appreciate it. Problem: An ant starts digging a tunnel. On the 1st day he digs 9m north. The 2nd day he digs 6 m east. The 3rd day he digs 4m south. He continues to dig in this pattern. Question 1: How far will he dig in total? Question 2: How far north from his starting point will he end up?"

Hi Jodi, this is definitely a fun problem. I'm going to answer these two questions, and then I'm going to pose two more questions for you to think about.

Question 1: How far will the ant dig?

Each day the ant digs 2/3 of what he dug the day before. Thus, his total distance is

Eq. 1: D = 9 + 6 + 4 + 8/3 + 16/9 + ...

Now, there are formulas you can use to calculate that sum, and if you're in a Pre-Calculus class (or higher) you probably know those formulas. I'm going to show you how to get that sum without a formula.  I'm going to take the equation and multiply it by 2/3:

Eq. 2: 2/3D = 6 + 4 + 8/3 + 16/9 + 32/27 + ...

Now, if I subtract the second equation from the first one, all but one of the terms on the right hand side of the equation cancel out, and  I get the following:

Eq. 3: D/3 = 9

This leads to D = 27, which is the answer to Question 1. If you want to make sure, pull out a calculator and punch in a bunch of these terms; you'll see that it doesn't take more than 7 or 8 terms for you to start getting close to 27.

Question 2: How far north from his starting point will he end up?

Before we get started, I'd like to point out that the problem seems just a tiny bit ambiguous. There are a couple ways I could read this:

1. The ant digs North, then East, then South, then repeats this pattern, going North, East, South, North, East, South, etc.
2. The ant digs North, then East, then South, then North, then West (completing the compass pattern) before repeating all four directions.

Strictly speaking, interpretation #1 is the precise reading of the problem, but I have a feeling interpretation #2 was intended, so I'm going to go with that one.

To solve this, we treat a distance south as a negative distance, and we look at the odd numbered terms of the original sequence (because the even numbered terms are east/west motions, and don't affect the north/south distance).

Eq 4: D_N = 9 - 4 + 16/9 - 64/81 + ...

This time the common ratio is negative (we know this because the terms are alternating signs). It is -4/9. So you can do the process I did above, multiplying the equation by -4/9 and then subtracting. Or you can use the formula I referred to above, but didn't tell you:

Eq 5: S = a/(1 - r), where a is the first term and r is the ratio.

D_N = 9/(1 - (-4/9)) = 9/(13/9) = 81/13

Question 3: What about the other digging pattern?

We made the assumption that the problem intended for the ant to dig in all four compass directions, but that may not have been the intent. What if the western direction is skipped each time? How does that affect the answer. It definitely makes it more interesting; I think you'll end up needing to treat it as two separate series: D_N and D_S, and then find the difference.

Question 4: What's the total displacement?

Displacement is a word we use a lot in Physics. It's different from the concept of distance (which is how far the ant traveled). Displacement is how far (and in what direction) the ant ended up from where he started, and it's a combination of the distance north, and the distance east. To find that answer, you would need to set up a D_E equation (distance east), and then do the Pythagorean Theorem on D_N and D_E to find the hypotenuse, which is the distance from his starting point to his ending point.

Since displacement is a vector (magnitude and direction) you'd also have to do a bit of trig to find the direction in which the ant ended up from his starting point.

Those are problems I'll leave you to contemplate. Thanks for asking!

Professor Puzzler

B.R. asks, "Can you explain what mechanical advantage is?"

Hi B.R., I'll give it a shot. Not knowing how much Physics background you have, I'll try to explain it in simple terms.

First of all, I'd like you to consider the following arrangement, which is a person pulling on a rope, which runs over a pulley, and down to an object with a weight of 400 Newtons (that's about 90 pounds, if you're used to using English units).

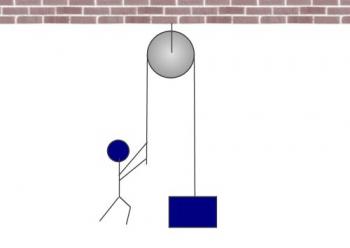
Now, when we talk about someone pulling on something, we're using the concept of a force.  Forces are measured in Newtons (or pounds). If the object has a weight of 400 Newtons, that means the person holding the rope has to pull with a force of 400 Newtons in order to keep the object from speeding up or slowing down. If he pulled with a force greater than 400 Newtons, the object would begin accelerating upward. If he pulled with a force less than 400 Newtons, the object would begin to accelerate downward.

This system has a mechanical advantage of 1. This means that on one end, the person applies a force that is equal to the force at the other end of the system. 400 / 400 = 1.

So let's take our pulley system and make it just a little more complicated. Here I've put a second pulley at the bottom, and attached the rope to the ceiling. The object hangs from the lower pulley. 

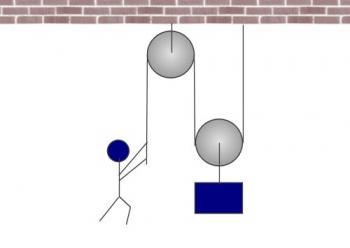
Now, one of the things that's important to understand is that if the man pulls with a force of 400 Newtons, there is tension in the rope, and the tension is the same everywhere along the rope. That tension is also measured in Newtons, and it is 400 Newtons. But here's where it gets interesting. Look at that lower pulley (that the object is hanging off). What is the tension in the rope to the left of the pulley? 400 N, right? What is the tension in the rope to the right of the pulley? It's also 400 Newtons. This gives a total of 400 + 400 = 800 Newtons. The upward force on the object is double the object's weight. This object is going to accelerate upward, even though in the first scenario, it would not have accelerated.

So if the man pulls with a force of 400 N, the output force is 800 N. The mechanical advantage is 800 / 400 = 2.

Incidentally, this means that the man could hold up an 800 Newton weight by applying a 400 Newton force. That's pretty impressive!

You could add more pulleys to the system, as shown here:

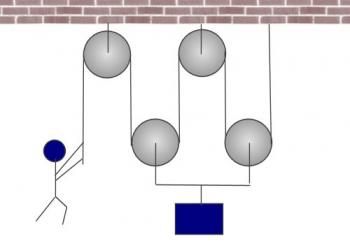
In this case, if the man is pulling with a force of 400 N, that means that there is 400 N of tension all through the rope, and so each of the lower pulleys has an upward force of 800 N, which means that the object (which is being supported from those two pulleys) has an upward force of 1600 N applied!

So the mechanical advantage is: 1600 / 400 = 4.

It seems like this is a win-win situation; you get better results by adding more and more pulleys. So why not add five hundred pulleys? If you did, you could hold up a 400 Newton object by applying a tiny, tiny force (less than 1 Newton!). So is it really a win-win situation? Not exactly. You see, there's a tradeoff for mechanical advantage. The tradeoff is the distance you pull the object. Take a look at the first diagram. If the man pulls the rope down 1 meter, the object will rise 1 meter. 

But what about the second diagram? What will happen there? Well, if the man pulls the rope down 1 meter, that meter is evenly distributed on either side of the lower pulley. Which means that pulley will only rise 0.5 meters. And therefore, if he pulls down a meter, the object only rises half a meter.

What about the third diagram? In that scenario, if the man pulls the rope downward 1 meter, that meter gets evenly distributed among four sections of the rope (one on either side of the two lower pulleys). In other words, the object only moves 0.25 meters.

So, if you had 500 pulleys, you'd be in the very interesting situation that you could easily lift a 400 Newton object, but it would take you a long time to do it; for every meter you pulled the rope down, the object would only move 2 millimeters!

There are many other kinds of machines: screws, wedges, levers, axle-and-wheels, and inclined planes. For every machine, there's a tradeoff; you can make the work easier, but in doing so, you end up extending that effort over a longer distance. An inclined plane is another easy one to picture. Imagine trying to lift a grand piano 1 meter straight off the ground. Can't do it, right? But if I made a long ramp, you could push the piano up. Much easier than lifting, but the tradeoff is that you have to push it a whole lot more than 1 meter!

First of all, I want to make it clear that not only am I not a bowling lane lubricant expert, I'm also not a bowling expert of any kind. I haven't been bowling in years. But your question reminded me of something that used to fascinate me as a teenager. We had a candlepin bowling place in town, and a group of teens from our church would often go there on a weekend evening to bowl.

There was an elderly little man named Harry who was always there. I used to watch him bowl with fascination. While everyone else was racing to the line and giving a powerful swing of the arm, little old Harry would waddle. I kid you not. It was almost painful to watch the snail's pace with which he would approach the line. And he was always holding the ball overhand instead of underhand like everyone else did. Basically he just walked up to the line with his arm hanging limply at his side.

And then, at the last moment, he'd give a flick of his wrist, and that ball would go skidding down the lane, and the pins would go flying. It was a strike every time. That little old man had perfect 300 score cards hung all over the walls of that place, and had won about every local bowling competition.

What was his secret? Well, I'm sure he had more than one, but here's one of Old Harry's secrets: backspin. Notice I said the ball skidded down the lane. Sure, it was rolling, but it was rolling backward, which meant it was really just floating in lane oil. What did that do for him? Consider the two images below.

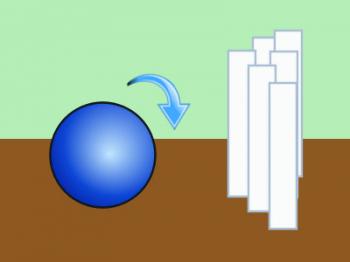
In the first image, we see a ball approaching the pins with a forward spin. You know what that ball is going to do to the pins? It's going to knock them down. But knocking pins down wasn't what happened when Old Harry was bowling. Take a look at the next picture, which shows a bowling ball approaching the pins with a reversed or back spin.

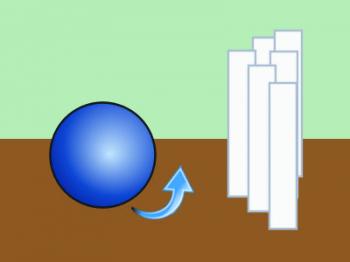
You know what that bowling ball is going to do? Sure, it's going to knock the pins over, but because of its spin direction, it was knocking those pins up. That backspin made the pins go flying everywhere. One pin flying upward would wreak a lot of havoc on the rest of the pins.

So what does this have to do with the lane lubricant? Simple. The lubricant lowers the coefficient of friction on the lane, which allows the ball to spin backward longer, before the spin slows to a stop and reverses to a forward spin (Try it sometime - send the ball down the lane with a backspin, and if the ball is multi-colored, you should be able to see the point at which it stops spinning backward and reverses to a forward spin). So if there was no oil on the lane, Old Harry's bowling ball would have reversed its spin before reaching the pins, and less havoc would have ensued.

And goodness knows, any time we can have havoc, we approve. :)

That coefficient of friction will also make a huge difference when it comes to sideways spins. Depending on how you release the ball, you can make the the ball do a nice "hook" at the last minute, and nail the pins at an angle.  This is an important technique.

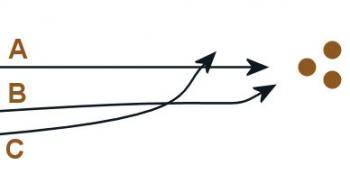
But when the ball hooks isn't just dependent on how you spin it; it's also dependent on the coefficient of friction. If there's no friction whatsoever (entirely theoretical - there's always friction), the spin will be completely irrelevant; the ball will go straight into the pins (line A). If the coefficient of friction is just right, the ball will do a combination of sliding and rolling, and hook at the very last moment (line B). Too much friction, and the hook happens too early, sending your ball careening into the gutter (line C).

But all of this depends on your having very good control of your release of the ball; for me, it was always a major accomplishment to have a frame without a gutter ball. Just a little piece of evidence that theoretical knowledge doesn't always give practical advantage!

Question: In your Gravity Train Simulator, you made the following statement: "If the train is inside the earth, the force of gravity acting on it is related not just to its distance from the center of the earth, but also on the amount of earth mass which is closer to the center of the earth than the train is." This seems to imply that all the mass outside the train's radius somehow cancels out. So if someone was in outer-space, inside an enormous steel shell - does that mean they would be weightless wherever they were in the shell? ~H. Borash

Answer: Yes, that's correct, H. To rigorously prove this, we would need to use a bit of Calculus, but I can show you a rough geometry approximation that'll help you see why it's true. First, a diagram. Here's a spherical shell. We'll assume it's absolutely enormous - big enough to enclose the earth and the sun. This hypothetical structure is called a Dyson sphere. I've marked the sun and the earth inside the sphere.

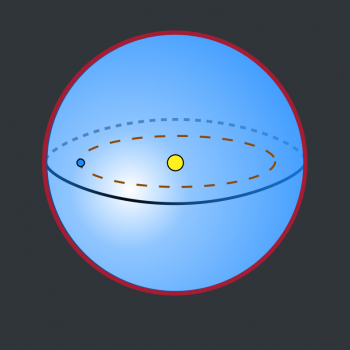
The yellow circle at the center of the sphere represents the sun, and the smaller blue circle to the left represents the earth. The brown dotted line represents the earth's orbit around the sun.

Obviously, this is not drawn to scale; it's difficult to make both the sun and earth to scale in a single diagram without the earth becoming nearly invisible. So I didn't even try.

But the question you asked is essentially equivalent to this: wouldn't the Dyson sphere throw the earth out of its orbit? That sphere has got to be incredibly massive, and planet earth is much closer to one side than the other. So wouldn't earth get dragged out of its orbit?

Or, to put it another way, if the sun wasn't there at all, and earth was motionless, would it stay motionless? Or would it get dragged toward the closer side of the sphere?

The answer to both questions is: No. No, the sphere would not drag the earth out of its orbit. No, earth would not go crashing into the sphere. All of the gravitational forces applied by the sphere on planet earth cancel each other out. Even though earth is not at the center of the sphere.

The reason is that because the earth is closer to one side, there is more mass on the other side, and the closeness of the mass on one side exactly cancels against the extra mass on the other side!

As I said above, a full, rigorous proof of this involves some Calculus, but I'm going to try to give you a non-calculus explanation that may help you visualize what's happening. I want to focus on two disks of the sphere - one close to the earth, and the other on the opposite side, furthest away from earth. To simplify, we're going to treat these as flat disks, so they don't exactly match the contour of the Dyson sphere:

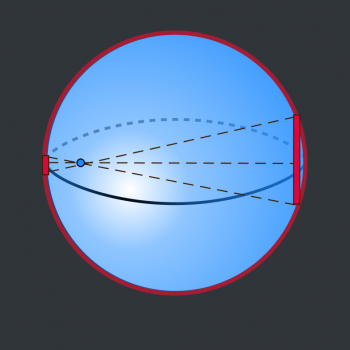
Notice how much bigger the disk on the right is, compared to the one on the left. That disk is much further away, so each cubic inch of that disk exerts less force on earth than a corresponding cubic inch of the closer disk.

On the other hand, you can easily see that the disk on the right contains many many more cubic inches than the disk on the left.

So maybe they cancel? Let's take a closer look.

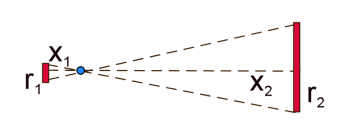
If we knew the thickness (h, for height) of the disk, as well as the density (D) of the material the disk is made of, we could calculate the masses (m₁ and m₂) of the two disks.

m₁ = hπr₁²D

m₂ = hπr₂²D

However, we have more variables than we need. Since we have some similar triangles, we can say that r₂ = r₁(x₂/x₁). This changes our second equation to: m₂ = hπr₁²(x₂²/x₁²)D.

Now this is where the magic happens: we're going to plug both of those masses into the gravitational formula:

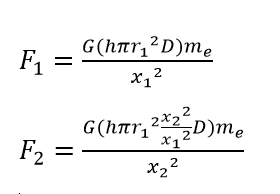
So even though one disk is much larger than the other, they both exert the same gravitational force on earth, canceling each other out!

Again, this is not a rigorous proof. Most proofs I've seen of this involve rings instead of disks, and doing integrals (calculus) to show that all the rings cancel. But this geometric demonstration hopefully helps you to see that it's a reasonable conclusion!

A visitor from Nigeria asks, "What is the different between aceleretion and velocity?"

Acceleration and velocity are two quantities that we deal with in the field of Physics. They are related, but quite different concepts. 

Let's start by talking about something acceleration and and velocity have in common. They are both vectors. Back when I was in school, students never heard of vectors until they hit high school Physics class, but nowadays, most kids learn what a vector is much earlier than that. And they don't learn it at school. They learn it while watching the movie "Despicable Me."

The character Vector announces to Gru that his name is vector because, "I commit crimes with both direction and magnitude."

A vector contains two pieces of information - a size (magnitude) and a direction. Velocity and acceleration are both vectors.

Another way in which velocity and acceleration are similar: they both relate to the motion of an object.

Velocity is a way of defining the motion of an object. It can be described as a speed and direction of motion. For example, a car is traveling at 60 mph East. 60 mph is the magnitude, and east is the direction. I'm in an elevator that is going down to the first floor at a speed of 5 m/s. 5 m/s is the magnitude, down is the direction.

So what is acceleration? Acceleration is the rate at which the velocity is changing. It is also a vector, so it also has a magnitude and a direction. For example, In the elevator example above, if the elevator had an acceleration of 1 m/s²up, that would mean that every second, the speed of the object is decreasing by 1 m/s. So after one second, the elevator would be traveling at 4 m/s. After two seconds, it would be traveling at 3 m/s. And after five seconds, it would be standing still.

On the other hand, if the elevator had an acceleration of 1 m/s² down, the elevator would be speeding up.

If the cable on the elevator broke, it would have a downward acceleration of 9.8 m/s². As you might imagine, that would be downright terrifying. After one second, the elevator would have a velocity of 14.8 m/s down. After two seconds, 24.6 m/s down, which is about 55 mph down. Obviously, there's a good reason to be concerned if the cable breaks!

If the elevator had an acceleration of 1 m/s² west, that would mean that as the elevator is dropping, it's also picking up speed in a horizontal direction, which - I suppose - means it's crashing through the side of the elevator shaft!

Any time the velocity is changing, you have an acceleration. If the velocity is not changing, the acceleration is zero.

When I'm teaching acceleration to my physics class, I always ask them how many accelerators their car has. They usually respond by saying, "The gas pedal." I tell them that's not the only one. They ponder for awhile, and then realize that the brake is also an accelerator; it gives an acceleration in the opposite direction of the motion. I tell them they're still not done, and remind them that velocity is a vector, which includes a direction, and that acceleration is the rate of change in velocity. Eventually, someone realizes that the steering wheel is also an accelerator, because it changes the direction of the car.