We recently had a blizzard up here in the north. We got 22 inches of snow, and although I've seen bigger storms, it's been a long time since I've seen one this big. You can see my boy here playing with his shovel on top of a newly plowed snowbank. You can put money on the fact that no one is going to be using that swingset behind him for a few months!

A friend commented that "it's snowing to beat the band," and then added that "to beat the band" is one of those strange English idioms that most of us can't even explain.

So let's try to explain it! Part of the difficulty with this idiom is that there are two words in it that can have multiple meanings:

Beat (verb)

• To strike violently (My child beat on that snowbank with his shovel.)
• To gain victory over (He beat us all in a game of "King of the Snowbank.")
• To pulsate (Climbing on top of snowbanks makes his heart beat faster!)
• To stir (You need to thoroughly beat the egg whites when making meringue.)

Band (noun)

• a loop designed to hold things together (a rubber band)
• a stripe (A mallard has a white band around its neck.)
• a range of frequencies (the AM band, the FM band, etc)
• a group of people with a common interest (Robin Hood's Merry Men were a band of bandits)
• a group of musicians performing together (Seventy-six trombones would make for a very large band.)

Now, with four different verb meanings, and five different noun meanings, our knowledge of counting principles helps us to determine that there are 20 different possible meanings for this idiom!

Maybe it means "to violently strike Robin Hood's Merry Men," or "to pulsate a mallard's neck," or "to stir the FM band."

Okay, these are all silly. The definitions we're looking for are "to gain victory over" and "a group of musicians performing together."

The earliest usages of the phrase involve someone playing a musical instrument or singing loudly enough to overpower a musical band. If you "sing to beat the band," that means you're singing loudly enough that people can hear you over the sound of the band playing. Generally, nowadays, we don't think about singing loudly enough to be heard over a band, because we have microphones to help amplify our voices. But the first print appearances of this phrase occured right around the time Edison and others were developing the microphone (and they were being used for recording purposes rather than for live performances).

Eventually, the phrase took on a more generic meaning. The phrase now simply suggests a superlative. When I say that my little girl talks to beat the band, I'm not saying she talks loudly; I'm saying that she talks a lot! Similarly, when I say that the snow is falling to beat the band, I'm not saying it's falling loudly! 

I should add that there is some argument out there that it's a variation on the phrase "beat Banagher" or maybe "beat Banaghan," both of which would be Irish references to...well, it seems that even the Irish aren't fully convinced, since they're not sure how to spell it! Regardless, the first print references we have make it clear that we're using the music definition of band, so the Banagh (er/an) controversy isn't terribly relevant to our understanding of the phrase!

Since it's almost the new year, this image (click the image for a larger view) is making the rounds on facebook again, and everyone is reading it and saying, "WHAT? How does that work out to $667.95?"

The answer is, it doesn't. It works out to exactly what you thought it would work out to: 365 pennies, or $3.65. Unless it was Leap Year, and then it would work out to $3.66. Not terribly hard math.

However, even though "a penny a day" is what they said, "a penny a day" is not what they meant. How do I know that? I'll show you in just a minute.

What they meant was, on January 1st you put in one penny. On January 2nd, you put in two pennies. On the 3rd, three pennies. And so on, until December 31st, when you put in 365 pennies, because it's the 365th day of the year.

How do I know that's what they meant? Because there's a really nice formula to calculate the sum of the first n integers:

Sum = n(n + 1)/2

In this case, n = 365, so the sum is:

Sum = 365(365 + 1)/2 = 66,795.

And that's how I know that's what they meant - because if that's what they meant, the math works out correctly to $667.95.

And by the way...if it was leap year?

Sum = 366(366 + 1)/2 = 67,161, or $671.61.

So yes, this will work out to save you a pretty good sum of money by the end of the year. Maybe enough to pay a month's rent, depending on where you live!

Of course, it's not as good as doubling the number of pennies each day; that would save you a boatload of money over the course of a year:

1 + 2 + 4 + ... + 2ⁿ = 2^{n + 1} - 1

So: 1 + 2 + 4 + ... + 2³⁶⁵ = 2³⁶⁶  - 1 = 1.5 x 10¹¹⁰.*

Actually, scratch my last comment; that's not a boatload of money. If a penny's volume is 0.35 cm³, or 0.00000035 m³, that's a volume of 5.25 x 10¹⁰³ m³. Considering the volume of the sun is 1.4 x 10²⁷ m³, I don't think you're going to fit those pennies in a jar, a boat, or even all the planets of the solar system. Maybe we should just stick to the original plan.

Incidentally, there's also a "Dollar a Week Challenge" in which you save one dollar the first week, two dollars the second week, and so on for an entire year. It sounds like a lot more, since you're saving a dollar instead of a penny, but there are only 52 weeks in the year, so it works out like this:

Sum = 52(52 + 1)/2 = $1,378, which is only a litte more than twice the penny challenge.

If you wanted to get really interesting, you could do a "Dollar Square Weekly Challenge," which would look something like this:

In the first week, you save 1² = 1 dollar.
In the second week, you save 2² = 4 dollars.

And so forth. It turns out, there's a nice formula for the sum of squares as well:

Sum = n(n + 1)(2n + 1)/6

Sum = 52(52 + 1)(2 x 52 + 1)/6 = $48,230. That's a lot of money! How would it compare to a Penny Square Daily Challenge?

Sum = 365(365 + 1)(2 x 365 + 1)/6 = 16,275,715 pennies, or $162,757.15. So even though the Dollar Challenge saves more than the Penny Challenge, the Penny Square Challenge saves more than the Dollar Square Challenge.

It would be interesting to see how many weeks you'd have to do the Dollar Square Challenge in order for it to surpass the Penny Square Challenge for a year. I'll leave that do the reader to figure out!

* This formula is actually for a leap year. Since the first term of the sequence is 2⁰, the 366th term is 2³⁶⁵.

It's my yearly tradition to take the number for the new year and see if I can find interesting mathematical novelties about the new year. 

The first thing I always do is check the prime factorization. It turns out 2017 is a prime number. So that's something novel, yet not extremely unusual, since there are an infinite number of primes. The previous prime year was 2011, and the next one is 2027.

Incidentally, since it is a prime, and it is one more than a multiple of four, Fermat's theorem on the Sums of Two Squares gives us an interesting conclusion: 2017 can be written as the sum of two perfect squares.

The two squares, in case you were wondering, are the squares of 9 and 44. 2017 = 9² + 44².

Can it be written as the sum of three perfect squares? Yes it can, as follows:

12² + 28² + 33²
18² + 18² + 37²
21² + 26² + 30²

For those who enjoy numerology, multiply the two numbers being squared in the second row above (18 and 37), and you'll get a beastly number (666). And you thought 2016 was bad.

Not that this is terribly unusual, but 2017 can be written as the sum of two palindromes:

2017 = 1331 + 686

Of course, I also like to see if I can find a ridiculously ugly way of writing it, and this year's looks like this:

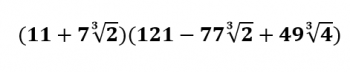
That looks appalling, I know. You're welcome to multiply it out, and you'll see that it works out to 2017. If you're wondering how I came up with that nasty thing, I did it by noticing the following:

2017 = 1331 + 686 (as mentioned above)
2017 = 11³ + 2×7³
2017 = 11³ + (7×2^1/3)³

And then it was just a matter of using the sum of cubes factoring rule:

a³ + b³ = (a + b)(a² - ab + b²)

It's interesting that 2017 can be written as a perfect square plus twice another perfect square (2017 = 37² + 2×18²) and it can be written as a perfect cube plus twice another perfect cube (2017 = 11³ + 2×7³).

Happy New Year!

PS - if you write your dates as m/d/y, you'll be looking forward to July 10, 2017, which is 7102017, another palindrome. Otherwise you'll be looking forward to October 7, 2017.

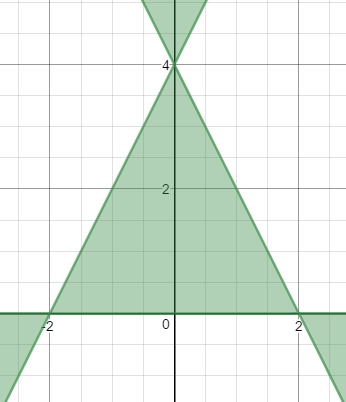
A follow-up question from this year's Christmas Graph Post: "You said we should be able to factor equation T (the Christmas tree outline equation). How?" - Kevin from Nebraska

Hi Kevin, first of all, for anyone who doesn't want to go find the equation in the other post, here it is:

Let T be the equation: 4x²y - y³ + 8y² - 16y ≤ 0

The first step in factoring this should be easy; every term on the left has a y in it, so we can factor that out:

y(4x² - y² + 8y - 16)

The next step is to split 4x² - y² + 8y - 16 into groups, in the hope that we can find a grouping that will help us factor it further. Grouping is not always a cut-and-dried process; sometimes it's easy to find a grouping that helps, sometimes it's hard. And, of course, sometimes it's impossible, which makes the process both frustrating (when you can't find a grouping that works) and satisfying (when you do!).

Typically, if I have four terms, the first thing I try is to split it into pairs, and factor each of the pairs:

(4x² - y²) + (8y - 16)
(2x - y)(2x + y) + 8(y - 2)

If the (y - 2) on the right matched either of the binomials on the left, we'd be able to factor this some more. Alas, no such luck. Let's try another grouping:

(4x² -16) - (y² - 8y)
4(x - 2)(x + 2) - y(y - 8)

Still no joy. Let's try another grouping:

(4x² + 8y) - (y² +16)

This one is also useless, because we can't factor the second group at all. At this point, I start re-evaluating my method; maybe grouping in pairs isn't the right way to go. Maybe I should create groups that are mismatched in size. For example:

4x² - (y² - 8y + 16) 

Suddenly, I realize, "Hey! That thing in the parentheses is a perfect square!"

4x² - (y - 4)² 

Wonderful! This is a difference of squares!

[2x + (y - 4)][2x - (y - 4)]
(2x + y - 4)(2x - y + 4)

So the full factorization is:

y(2x + y - 4)(2x - y + 4) ≤ 0

Now you can go back to the page for the Christmas tree graph and see why this graphs as shown at the top of this post.

Merry Christmas from me and my four year old son. Here's a Christmas tree ornament we built this morning. Each face is a triangle, and there are twenty faces in all. The faces are all made from last year's Christmas cards, cut into circles, and then folded around the shape of an equilateral triangle, in order to simultaneously form the face and provide a surface for gluing. Click the image for a larger view.

The icosahedron is one of 5 Platonic solids (regular solids). The complete list is:

• Tetrahedron: Four sides that are all equilateral triangles
• Cube: Six sides that are all squares
• Octahedron: Eight sides that are all equilateral triangles
• Dodecahedron: Twelve sides that are all regular pentagons
• Icosahedron: Twenty sides that are all equilateral triangles

I've made ornaments/decorations from three of those five shapes; maybe when I've done all five I'll publish an instruction sheet for each!

Merry Christmas!