It's my yearly tradition to take the number for the new year and see if I can find interesting mathematical novelties about the new year. 

The first thing I always do is check the prime factorization. It turns out 2017 is a prime number. So that's something novel, yet not extremely unusual, since there are an infinite number of primes. The previous prime year was 2011, and the next one is 2027.

Incidentally, since it is a prime, and it is one more than a multiple of four, Fermat's theorem on the Sums of Two Squares gives us an interesting conclusion: 2017 can be written as the sum of two perfect squares.

The two squares, in case you were wondering, are the squares of 9 and 44. 2017 = 9² + 44².

Can it be written as the sum of three perfect squares? Yes it can, as follows:

12² + 28² + 33²
18² + 18² + 37²
21² + 26² + 30²

For those who enjoy numerology, multiply the two numbers being squared in the second row above (18 and 37), and you'll get a beastly number (666). And you thought 2016 was bad.

Not that this is terribly unusual, but 2017 can be written as the sum of two palindromes:

2017 = 1331 + 686

Of course, I also like to see if I can find a ridiculously ugly way of writing it, and this year's looks like this:

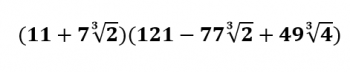
That looks appalling, I know. You're welcome to multiply it out, and you'll see that it works out to 2017. If you're wondering how I came up with that nasty thing, I did it by noticing the following:

2017 = 1331 + 686 (as mentioned above)
2017 = 11³ + 2×7³
2017 = 11³ + (7×2^1/3)³

And then it was just a matter of using the sum of cubes factoring rule:

a³ + b³ = (a + b)(a² - ab + b²)

It's interesting that 2017 can be written as a perfect square plus twice another perfect square (2017 = 37² + 2×18²) and it can be written as a perfect cube plus twice another perfect cube (2017 = 11³ + 2×7³).

Happy New Year!

PS - if you write your dates as m/d/y, you'll be looking forward to July 10, 2017, which is 7102017, another palindrome. Otherwise you'll be looking forward to October 7, 2017.