Lavinia from Italy writes: "Hi professor. I have just read your post about this year's number (2017). In this post you say that we can write 2017 as a the sum of one cube plus twice another. 2017 = 11³ + 2 · 7³ I was wondering how you managed manage to discover this. Did you use a formula or something? Thanks, Lavinia"

Thanks for asking, Lavinia. For those who missed it, this is a reference to the following blog post: Happy New Year 2017. In this blog post I make mention of the fact Lavinia pointed out:

2017 = 11³ + 2 · 7³

So how did I discover this odd fact? There wasn't a formula. I found it simply by playing around with the numbers to see what interesting things I found. I don't remember exactly what I was doing when I discovered that, but it probably involved a spreadsheet. I probably was thinking, "I wonder what results I'll get if I subtract perfect cubes from 2017!"

So I probably entered the following formula into cell A1 of a spreadsheet:

= ROW()^3 (cube the row number)

And then, in B1 cell put the following formula:

= 2017 - A1

Then I would have used the "fill down" feature to populate a bunch of rows with the results of those calculations:

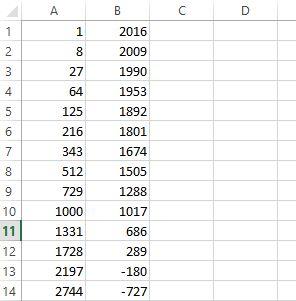
Incidentally, this time as I looked at the rows of numbers, I realized that there's a perfect square in the second column: 289 = 17². So we can also write:

2017 = 12³ + 17²

I probably did something very similar to find the perfect squares that add to 2017:

A1 = ROW()^2
B1 = 2017 - A1
C1 = SQRT(B1)

This would have given the following:

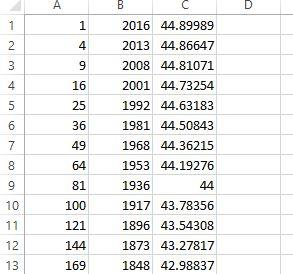
2017 = 9² + 44²

Incidentally, there was another row that had no decimal, further down the spreadsheet. It was row number 44, of course!

Excel (or any other spreadsheet application) can be a great help in exploring mathematical oddities. I realize that I'm a bit spoiled, having calculators and spreadsheets to use when playing with numbers. Imagine trying to figure out quirky number facts like these without even a calculator!