Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!

Good morning, and happy 3rd day of Christmas. I don't have any French hens for you, but I do have a bit of a Christmas puzzle for you to work out. The first person to submit a 100% correct solution will win a Pro Membership on the site, which gives you access to many features that aren't publicly available (like creating your own mazes, interactive word games, and more).
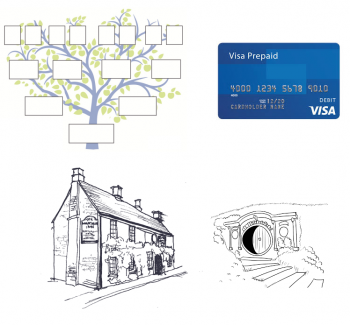
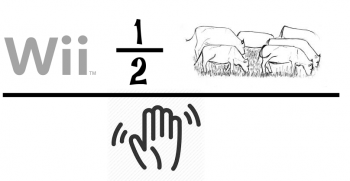
So here's the puzzle. Every year we fill stockings on Christmas Eve. This year I had a problem - one of the items for my wife's stocking was too big to fit in the stocking. So I wrote instructions for where she was supposed to find the gift. But I didn't put the instructions in her stocking. Oh no, that would be far too easy. I cut the instructions up into six pieces (being careful to cut them in such a way that it would be difficult to interpret the instructions if even one piece was missing) and hid them in various places around the house.
Then I created five rebus puzzles, which - when solved - gave the clues to where the puzzle pieces were located. The rebus puzzles were then taped to various items in her stocking, so she would discover them one at a time as she unloaded her loot.
The rebus puzzles are below. Before trying to solve them, you should know that they are all references to items that are in our home. One of them is an item that is only in our home around Christmas time. Most of them are items that are in everyone's homes. One item, I will tell you, is a map hanging on our wall. So to solve that rebus, you have to be able to tell me the location shown in the map. Another puzzle might require a google search.
Click on any picture to get a bigger version. When you think you know all six objects, click the "Ask your question" link at the top of bottom of the page to submit your answer. Once someone has solved all the puzzles, I'll post a note to that effect in this blog post. Sometime in January I will post the solutions to the rebus puzzles. Merry Christmas!
And by the way, if you enjoy rebus puzzles, there are books available on Amazon that have hundreds of these puzzles! Here's one that has over a thousand rebus puzzles:



Joshua asks, "I heard people say that a sum of two squares is (x + y + sqr(2xy))(x + y - sqr(2xy)) But I also heard that a sum of two squares is (x+iy)(x-iy) Are both of these correct?? And are there other ways to factorize the sum of two perfect squares?"
Hi Joshua, the process of factorization is the process of breaking down an expression into two or more expressions which, when multiplied together, give the original expression. So is it possible to factor something in more than one way? It surely is. Consider the following expression: 12. I know, it's a boring expression; it doesn't even have any variables. But it's still an expression, and it can be factored in many ways: 1 x 12; 2 x 6; 3 x 4; 2 x 2 x 3; -2 x -6 ... it can even be factored as 0.5 x 24. Usually when we're talking about factoring numbers, we think about integers, but our definition doesn't require that. So yes, there may be multiple ways to factor an algebraic expression. Some of them will be prettier than others, and sometimes the factorizations we find may not be at all useful, but that doesn't change the fact that they exist. Typically, when we talk about factorizations, we're looking for polynomial factors with real coefficients, and neither of the factorizations you gave fit that description, but they're still factorizations if they multply to the given expression.
So with that as background, let's take a look at your two expressions and see if they really are factorizations of x2 + y2. The best way to do that is to multiply the factors together and see what happens.
Expression #1
(x + y + √(2xy))(x + y - √(2xy))
x((x + y - √(2xy)) + y((x + y - √(2xy)) + √(2xy)((x + y - √(2xy))
(x2 + xy - x√(2xy)) + (yx + y2 - y√(2xy)) + (x√(2xy) + y√(2xy) - 2xy)
x2 + y2
So, yes, that is a valid factorization of x2 + y2. Let's try the other.
Expression #2
(x + iy)(x - iy)
x( x - iy) + iy(x - iy)
x2 - ixy +iyx - (-y2)
x2 + y2
More Factorizations?
Is there another factorization? Can we find it? Sure we can! Here are a couple possibilities:
x2 + y2 = x2(1 + (y/x)2)
x2 + y2 = (√(x2 + y2 + 4) + 2)((√(x2 + y2 + 4) - 2)
Again, these are not likely to be useful factorizations, but they still fit the definition of a factorization. In closing, I should point out that if, as I mentioned earlier, we're looking for polynomial factors with real coefficients, then x2 + y2 is irreducible, which is a fancy way of saying that it can be written only one way:
x2 + y2 = 1(x2 + y2).
Sixth grader Larry asks, "Is there distributive property in Star Operations...."
Good morning, Larry. Before answering your question, I'd like to give a bit of background on Star Operations, in case someone is not familiar with them. If you're not interested in background, you can skip to the horizontal bar, where I'll try to answer your question.
Star Operations are arbitrarily constructed operations in which a definition is given for how the operation is performed between two variables. They are referred to as "star operations" because the asterisk is often used as the symbol for the operation. For example, here is a star operation definition:
a * b = a2 + b2.
I had a student ask me once what these operations are good for, and my answer was, "They're good for teachers who like to torment students." That was, of course, a bit tongue-in-cheek, but the primary purposes they serve are:
- Giving students practice with arithmetic/algebraic manipulation
- Introducing the concept of functions, without actually using the word or symbolism of functions. The star operation given above can also be written as:
f(a, b) = a2 + b2.
With that as background, let's get to Larry's question.
For the sake of this discussion, let's use the star operation given above: a * b = a2 + b2. Larry wants to know if the distributive property works for star operations, so let's give it a try and see what happens. We kind of need to guess how a distributive property would be implemented - there are several possibilities, which I'll list below:
- a(x * y) = ax * ay
- a * (x + y) = a * x + a * y
- a * (x * y) = (a * x) * (a * y)
In the first case, the addition was replaced with a star. In the second, the multiplication was replaced with a star, and in the third, both the addition and the multiplication were replaced with a star. Let's test each of these by plugging in values for a, x, and y. If the values we pick work, that doesn't prove that the rule is legitimate, but if the values don't work, we know that the rule is bogus. Let's do the following values:
a = 3; x = 4; y = 2.
Possibility #1
3(4 * 2) = 3(4) * 3(2)
3(16 + 4) = 12 * 6
3(20) = 144 + 36
60 = 180, which is NOT true, so the first possibility is bogus
Possibility #2
3 * (4 + 2) = 3 * 4 + 3 * 2
3 * 6 = (9 + 16) + (9 + 4)
9 + 36 = 25 + 13
45 = 38; also bogus!
Possibility #3
3 * (4 * 2) = (3 * 4) * (3 * 2)
3 * (16 + 4) = (9 + 16) * (9 + 4)
3 * 20 = 25 * 13
9 + 400 = 625 + 169
409 = 794; BOGUS!
So we tried all the possibilities, and none of them worked. That doesn't mean that they are bogus for all star operations. However, it doesn't work for all star operations, it's not really good for much, is it?

"Good morning, I've been seeing some things lately about Donald Trump being in the Bible. Here are a few:
King Cyrus was in Isaiah 45, and Trump is the 45th president, so Trump is the 'new' Cyrus.
Donald Trump was born 700 days before Israel declared independence.
777 days after Donald Trump's birthday, Israel was 77 days old.
Israel's 70th anniversary will come exactly 700 days after Donald Trump's 70th birthday.
Donald Trump won the election on Netanyahu's 7th year, 7th month, 7th day in office.
What does all this mean?"
First of all, none of these things can be described as "Donald Trump being in the Bible." Most of them mention Israel, but the word "Israel" does not automatically make it a "Bible statement." With that in mind, let's talk about these three statements (I know, you're probably thinking "There are five statements, not three!" - you'll see why I say "three").
Statement 1: King Cyrus is discussed in Isaiah 45. He's also discussed in: II Chronicles 36, Ezra 1, 3, 4, 5, and 6, Isaiah 44, Isaiah 45, Daniel 1, 6, and 10. So unless you want to suggest that the first, third, fourth, fifth, sixth, tenth, thirty-sixth, and forty-fourth presidents are also the "new" Cyrus, there's not much point to this statement. Even if you limited it to Isaiah, or limited it strictly to passages that are prophecies, Isaiah 44 comes before Isaiah 45, so that would make Obama the "new" Cyrus.
Statements 2.0, 2.1, and 2.2: These statements are all identical. Once you've stated that Israel declared independence 700 days after Donald Trump's birth, the next two sentences add no new information; they are mathematical restatements of the same equation. The fact that your source had so little clever numerology to share that they had to state the same fact three different ways seems a bit suspicious.
Statement 3: Uh...no? According to several sources, Netanyahu took office (for the second time) on March 31st, 2009. So if his first year in office was 2009, his seventh year was 2015, not 2016. Besides, even if the math had worked out correctly, why did we go to his second term, instead of his first, or third, or fourth?
There are some good lessons to learn here.
- Fact-checking is critical. Statement 3 doesn't pass even a basic fact-check attempt.
- In addition to fact-checking, we must also be able to look at the "bigger picture". The first statement you shared passes the "fact-check" test; Isaiah 45 really is about Cyrus. But the bigger picture is that Cyrus prophecies also exist elsewhere, so 45 is not a special case.
- Sometimes basic mathematical understanding will help keep you from getting "conned" - algebraic understanding lets you see that the middle statements are all the same statement.
- Be wary of statements about x number of months or years ago, because people trying to find interesting connections have a lot of flexibility in how they count. For example, how do you count a year? 365 days? Or are you going to include leap years? Or are you going to simply subtract one from the year number? The answer is: you count it whichever way gives you an interesting result. Similarly, how do you count a month? 30 days? 31? Or do you revert back to the same day a month previous? Do you count your days back FIRST and then your months? Or vice-versa? It actually matters. For example, 7 months and 77 days before November 30th is either February 13th or February 14th, depending on which order you subtract (I'll leave it to the reader to figure out why). Which way do you do it? There is no standard rule, so you do your subtraction, and if it doesn't produce any interesting gems, you cheat and do the subtraction a different way, and you keep doing that until you find something "interesting"
- It's extremely easy to use a date calculator and a "what happened on this date" webpage to find events that seem to "prove" something. For instance, did you know that 666 days before President Trump was elected, ISIS perpetrated a hack against the US Central Command, and 666 weeks before the election, Russian hackers performed a distributed denial of service attack against US interests? Furthermore, 666 months, 666 weeks, and 666 days after Donald Trump's birth, terrorists committed the largest single attack in French history. Do I think that "means" anything? No, I really don't. But I think it means exactly as much as the random facts that someone shared with you.
Incidentally, if you're fascinated by this kind of numerology stuff (and why wouldn't you be? Numerology has managed to incorrectly predict the end of the world about a billion times in the last two thousand years!), you should be an equal-opportunity numerologist; for every web page you find that "proves" through numerology that President Trump is the second coming of a Persian-king-who-was-never-promised-a-second-coming, you can find another web page that "proves" through numerology that he is the anti-Christ.
Numerology is a fascinating subject, but I've studied math and probability for far too long to be swayed by the numerical coincidences that happen on a daily basis around us!

This morning's question is, in essence, if you know the probability of an event happening, what is the probability of it NOT happening?
To answer this question, it's good to remember that a probability is a ratio. It is: [number of desired outcomes] : [total number of outcomes] (assuming that all outcomes are equally likely).
Let's consider the flipping of a coin. Suppose you want the probability of getting heads. The number of desired outcomes is 1. The total number of outcomes is 2.*
'So the probability is 1/2. So what is the probability of NOT getting heads? Well, that's the same as the probability of getting tails. Desired outcomes: 1, possible outcomes 2. Thus, the probability is also 1/2.
* I've had students argue that a coin could land on its rim, so there are actually 3 possible outcomes. I point out to them that there are a couple problems with that. First, if it lands on the rim, we re-roll the coin, so that really doesn't count. Second, if we decided to keep that roll, we can't use our ratio definition above, because all outcomes are not equally likely.
So now let's switch gears and talk about a six-sided die. What is the probability of getting a perfect square when you roll the die? Well, there are 2 perfect squares that are possible results: 1, and 4. So desired outcomes = 2, total outcomes = 6. Thus the probability is 2/6 (we can simplify that to 1/3, but for now I'd like to keep in the form 2/6).
What is the probability of NOT getting a perfect square? Well, there are 4 numbers that aren't perfect squares: 2, 3, 5, and 6. Desired outcomes = 4, total outcomes = 6. Probability is 4/6.
Let's try one more example. What is the probability of rolling a total of 12 if you roll two six-sided dice?
There is only one way to get a sum of 12: you need a six on each die. There is a total of 6 x 6 = 36 possible outcomes. Desired = 1, Total = 36, probability = 1/36. What about the probability of NOT rolling a 12? Well, you could list off all the possible outcomes, but let's reason this out instead. If there are 36 possible outcomes, and only one of them leads to a sum of 12, how many don't lead to a sum of 12? The answer should be fairly obvious: 36 - 1 = 35. Desired = 35, total = 36, probablity = 35/36.
Now let's put those results together:
Coin: 1/2; 1/2
Die: 2/6; 4/6
2 Dice: 1/36; 35/36
Hopefully you can see a pattern here: in each case, the probabilities add to 1. And, if you think about how we reasoned out the example with two dice, that should make sense to you; every outcome is either a desired or a not desired outcome. There are no other options. So when you add together those options, you get the total number of outcomes. And [total outcomes]/[total outcomes] = 1.
We can write this rule as an equation like this: P(x) + P(~x) = 1.
In words: The probability of x, plus the probability of NOT x equals 1.
I hope that helps!


