"I hate converting degrees to radians and the other way. Degrees seem simpler why can't we just stick to that?"

Good question! Degrees have been around for a long time. There are varying theories about where the unit originated. Some suggest that 360 comes directly from the Babylonians' sexagesimal (base 60) system; 360 = 6 x 60.

Others suggest that 360 was chosen because it is (approximately) the number of days in a year. Thus, a degree is roughly the angle traversed by the earth in a single day.

One thing that is certainly true: in the days before calculators, having units based around highly composite number would have been convenient for division purposes. 360 is highly composite, having 24 factors. Look at it this way. If you wanted to divide a circle in half, thirds, fourths, fifths, sixth, eighths, tenths, twelfths, fifteenths, sixteenths (and many others) you could do so without having any decimals to deal with.

That's great, although having calculators makes that less important to mathematicians than it once was.

So that's where degrees came from. What about radians?

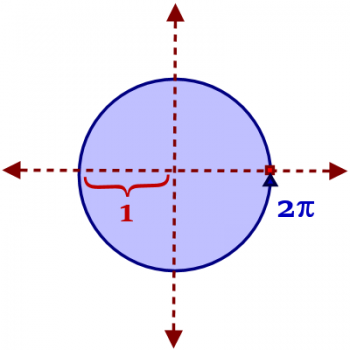
Radians come directly from a unit circle. When we talk about the unit circle, we're talking about a circle with radius 1, centered at the origin of the cartesian plane. If you look at the picture, you can see that the radius of the circle has been marked as 1 unit. Now look at the blue line, starting with the red beginning, and going all the way around the circle to the blue arrow. How long is that curved segment?

The answer to that question comes from the formula C = πd - the circumference is pi times the diameter. What is the diameter? It's twice the radius, or 2 x 1 = 2. Thus, the circumference is 2π. With that in mind, a rotation around the circle could be thought of as an arc-length around a unit circle.

Okay, so that's where radians come from - but it doesn't answer the question of why we use them. It does seem like 30º is easier to deal with than π/6, and 270º is easier to deal with than 3π/2. So why deal with radians at all?

Because, as you move through more advanced topics in mathematics, you'll discover that there are certain relationships that only work if you're using radians instead of degrees. Consider the infinite summation below:

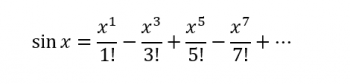
This beauty only works if x is in radians; if it's in degrees, it does not work!

But pretty formulas aren't the only reason radians work better. Especially if you're dealing with rotational motion (a car's tires, for example), writing things in radians keeps it simple. Consider the following examples:

#1: A car's tires have a radius of 12 inches. Its rotational speed is 30 degrees per second. How far does the car go in 1 second?

#2: A car's tires have a radius of 12 inches. Its rotational speed is 0.5326 radians per second. How far does the car go in 1 second?

#1 Solution: To find the distance the car has traveled, we divide 30 by 360 to find out what fraction of the circle we've rotated. Then we multiply that fraction by pi and the diameter of the circle to get the distance traveled: 12 x 2 x 30 x π / 360 = 6.3912 inches.

Now, before we look at problem #2, It's important to notice that in your calculations you've multiplied by 2π, and divided by 360. That's 2π/360, which is the same as π/180. That should look familiar to you; it's the conversion factor to swap from degrees to radians. In other words, even though you didn't realize you were doing it, you converted degress to radians in order to solve the problem! Now let's look at the solution to the second problem (which, by the way, is identical to the first, just using different units).

#2 Solution: To find the distance traveled, multiply the radius by the rotation in radians: 12 x 0.5326 = 6.3912 inches.

Wasn't that solution much simpler? You didn't have to do any conversion factors; you just multiplied the radius times the angle! That's pretty sweet!

So, yes, it's a nuisance to have two different units (just be glad you don't have to throw gradians into the mix!), but in the long run, your mathematical and scientific life will be simplified by making the π/180 switch to radians!