Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Wesley writes, "Is there a better way of factoring polynomials other than guess and check? For example: factoring 21x5 - 2x2 + 4x - 1, you probably will have to guess and check what goes in the parentheses. It could be (3x - something)(7x + something)(x - something)..., or, it could be something entirely different. Aside from the limited equations like difference of squares, or sum/difference of cubes, I would like to know if it is possible to not have to guess and check. If you do not know of a solution, thank you anyways for your time."
Hi Wesley, In addition to the rules that you mentioned, you can find a few more rules here, including sum/difference of odd powers, sum of even powers, grouping, and something I like to call aggressive grouping.
If none of those help, another tool that might help you out is something called the Rational Root Theorem. The rational root theorem says that if a rational zero to a polynomial exists, then written in simplest form p/q, p is a factor of the constant, and q is a constant of the highest order coefficient.
How does this help in factoring? Well, if p/q is a zero of the polynomial, then (qx - p) is a factor.
It's important to note that the statement above has a big "if" in it. It's possible that no rational roots exist. But if they do exist, this rule helps us out in our trial-and-error search by eliminating possibilities.
Let's take an example: 3x3 - 5x2 - 42x - 40 = 0.
The rational root theorem tells us that if this has rational roots, they are of the form p/q, where p is a factor of 40, and q is a factor of 3. Now, this still gives us a LOT of possibilities to consider, because p could be 1, 2, 4, 5, 8, 10, 20, or 40 (plus the opposites of all of those), and q could be either 1 or 3 (or their opposites).
So let's start with something that's not a fraction: Let's try 1, and see what happens. I'm going to do synthetic division on this. If you don't know how synthetic division works, you'll want to take a look at this explanation: How to do synthetic division.
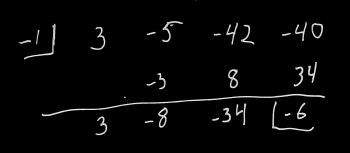
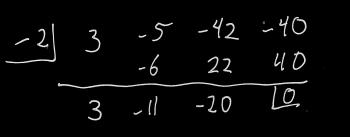
The next bit of good news is that we can use the values in our synthetic division to reduce the polynomial by the factor we just found: our polynomial can be rewritten as (x + 2)(3x2 - 11x - 20) (note the numbers at the bottom of our synthetic division - they are the coefficients of the reduced polynomial). To find our next factors we can use the techniques that we're familiar with on the factor 3x2 - 11x - 20, or we can continue doing synthetic division.
Of course, I cheated; I created a polynomial which I knew could be factored, but there's no guarantee that a given polynomial is factorable over real numbers, let alone rational numbers! Your polynomial, for example, has only one real root, and that one real root is not rational. If you had tried the rational root theorem on this, you would have tried 1, 1/3, 1/7, 1/21, and the opposites of all of those, only to find that none of them work. The good news is that because of the rational root theorem, you KNOW that you're done looking for rational roots.
So there are a few more tools for your arsenal; I hope something here was helpful!
Joshua asks, "I heard people say that a sum of two squares is (x + y + sqr(2xy))(x + y - sqr(2xy)) But I also heard that a sum of two squares is (x+iy)(x-iy) Are both of these correct?? And are there other ways to factorize the sum of two perfect squares?"
Hi Joshua, the process of factorization is the process of breaking down an expression into two or more expressions which, when multiplied together, give the original expression. So is it possible to factor something in more than one way? It surely is. Consider the following expression: 12. I know, it's a boring expression; it doesn't even have any variables. But it's still an expression, and it can be factored in many ways: 1 x 12; 2 x 6; 3 x 4; 2 x 2 x 3; -2 x -6 ... it can even be factored as 0.5 x 24. Usually when we're talking about factoring numbers, we think about integers, but our definition doesn't require that. So yes, there may be multiple ways to factor an algebraic expression. Some of them will be prettier than others, and sometimes the factorizations we find may not be at all useful, but that doesn't change the fact that they exist. Typically, when we talk about factorizations, we're looking for polynomial factors with real coefficients, and neither of the factorizations you gave fit that description, but they're still factorizations if they multply to the given expression.
So with that as background, let's take a look at your two expressions and see if they really are factorizations of x2 + y2. The best way to do that is to multiply the factors together and see what happens.
Expression #1
(x + y + √(2xy))(x + y - √(2xy))
x((x + y - √(2xy)) + y((x + y - √(2xy)) + √(2xy)((x + y - √(2xy))
(x2 + xy - x√(2xy)) + (yx + y2 - y√(2xy)) + (x√(2xy) + y√(2xy) - 2xy)
x2 + y2
So, yes, that is a valid factorization of x2 + y2. Let's try the other.
Expression #2
(x + iy)(x - iy)
x( x - iy) + iy(x - iy)
x2 - ixy +iyx - (-y2)
x2 + y2
More Factorizations?
Is there another factorization? Can we find it? Sure we can! Here are a couple possibilities:
x2 + y2 = x2(1 + (y/x)2)
x2 + y2 = (√(x2 + y2 + 4) + 2)((√(x2 + y2 + 4) - 2)
Again, these are not likely to be useful factorizations, but they still fit the definition of a factorization. In closing, I should point out that if, as I mentioned earlier, we're looking for polynomial factors with real coefficients, then x2 + y2 is irreducible, which is a fancy way of saying that it can be written only one way:
x2 + y2 = 1(x2 + y2).
"I can find the LCM of two numbers (like the LCM of 32 and 20 is 160), but how do you find the LCM if there are variables (like 32x2y and 20y3)?"
Before addressing your question, I'd like you to think, for a minute, about how you find the LCM of two numbers. When you were in elementary school, you may have been taught to list multiples until you find one that matches:
32: 32, 64, 96, 128, 160
20: 20, 40, 60, 80, 100, 120, 140, 160
This is fine, and is probably one of the easiest ways for children to visualize what it means that a number is the least common multiple. But since you're talking about variables, you're ready to approach LCMs in a slightly different way. If you already do LCMs the way I'm going to show below, please bear with me while I review it.
When I want to find the LCM of two numbers, I generally start by doing a prime factorization of the two numbers. You can use a factor tree, or whatever method you've learned. I get the following result:
32 = 25
20 = 22 · 5
With this factorization, finding the LCM is a cinch. First, the LCM must have both 2 and 5 as factors. Why? Because it's a multiple of numbers that have 2 or 5 (or both) as factors. So I can say:
LCM = 2? · 5?
What are those question marks for? They're there because even though I know the LCM has both 2 and 5 as factors, I haven't figured out what the exponents of those factors are. It's actually pretty simple to figure out, though; we compare the exponents of each factor in the two prime factorizations, and we take the larger exponent. Thus, since we have 25 and 22, 5 is the bigger exponent, and since we've just got 51 in the second factorization, that's the exponent we'll use for 5.
LCM = 25 · 51 = 160
Now, maybe you think that process is a lot slower than the other process. Maybe. Or maybe it just seemed that way because I was explaining each step. On the other hand, if you have the numbers 1008 and 1012, finding the LCM by the elementary method is going to be brutal (the result is 255024, and you'll have to list out 253 multiples of 1008 and 252 multiples of 1012).
But whether or not it's "easier" isn't actually the point. The point is that this method helps us answer your question about LCMs involving variables.
What are the prime factorization of 32x2y and 20y3?
32x2y = 25 · x2 · y
20y3 = 22 · 5 · y3
So the LCM has to contain the factors 2, 5, x, and y. And which exponents do we use? The higher exponent for each factor:
LCM = 25 · 5 · x2 · y3 = 160x2y3.
As a bonus, this method also allows us to find the LCM of some polynomial expressions. For example, find the LCM of x2 + 2x + 1 and x2 + 3x + 2. As with the previous problems, we begin by factoring:
x2 + 2x + 1 = (x + 1)2
x2 + 3x + 2 = (x + 1)(x + 2)
What is the LCM? It's (x + 1)2(x + 2)
"Good day sir, pls sir I need explanation on how to solve an equation like this x4 - 3x2 + 2. although I don't have problem on factorization but I don't know what to do when the power of "X" is greater than 2. looking for your reply Sir"
I can give you several answers to this question. One is a short quick answer that works for this problem. The other answers are more detailed, and give you more information than you need to solve this specific problem. Let's start with the short answer.
Short Answer
Notice that all the exponents in this expression are even. This means that we could do a substitution like this: y = x2. Doing this substitution changes the expression to:
y2 - 3y +2
As you said, you know what to do when it's a quadratic (the highest exponent is 2). This factors as follows:
(y - 1)(y - 2)
But wait - you're not done, because the problem had x in it, not y, so you have to put the x's back in:
(x2 - 1)(x2 - 2)
Now that you've substituted x back in, you should realize that one of those can be factored:
(x - 1)(x + 1)(x2 - 2). And that's your factorization. Technically, that's your factorization over rationals; if you're including irrationals, the second binomial can be factored as well:
(x - 1)(x + 1)(x - √2)(x + √2)
Longer Answer
The method shown above doesn't just work if the exponents are 4 and 2; they also work if the exponents are 6 and 3, or 10 and 5, or any other such combination. If you wanted to get really ugly, I suppose it would also work if you had fractional exponents like 5 and 5/2. The method works if it's a trinomial (three terms) and the exponent of the highest degree term is twice the exponent of the middle term, and the lowest degree term is a constant. For example, consider this one:
x6 + 8x3 + 12
We'll substitute y = x3.
y2 + 8y + 12
(y + 6)(y + 2)
(x3 + 6)(x3 + 2)
Of course, if you were factoring over reals, and you happen to know the rule for factoring a sum of cubes, you could factor this further. But since you mentioned not knowing what to do for exponents larger than two, we can save that for another day!
Similarly, if it was x10 +8x5 + 12, you would do the substitution y = x5.
Longest Answer
Again, this only works for trinomials under certain circumstances. But what if the expression doesn't match those criteria? Let's take an example:
x3 + 5x2 - 2x - 10
In this case, we can't do a substitution to simplify it, so we'll try doing some grouping. Since there are four terms, I decide to try breaking it into two groups of two terms each:
(x3 + 5x2) - (2x + 10)
Now we can factor each group:
x2(x + 5) - 2(x + 5)
Oh! Since both binomials in parentheses are the same, we can rewrite this as:
(x2 - 2)(x + 5).
This technique sometimes works. Sometimes grouping works only if you get creative in your groupings. Sometimes you need to rearrange the terms. Sometimes you might need to group them into groups of three terms, or groups of four terms.
Here's an example of rearranging terms:
x3 + 3x2 + 3x + 1
(x3 + 1) + (3x2 + 3x)
(x + 1)(x2 - x + 1) + 3x(x + 1)
(x + 1)(x2 + 2x + 1)
(x + 1)3
Confession Time
When I first saw your problem I did not come up with the simple solution. I wasn't paying attention, I guess, and my first thought was: I'll do this by grouping. I know. I made it harder than it really is. But even when you make a problem harder than it really is, sometimes you can come up with something interesting. In this case, I looked at your expression and rewrote it splitting the middle term into two pieces* like this:
x4 - 3x2 + 2
x4 - x2 - 2x2 + 2
(x4 - x2) - (2x2 - 2)
x2(x2 - 1) - 2(x2 - 1)
(x2 - 2)(x2 - 1)
(x2 - 2)(x - 1)(x + 1)
And I got the same answer, even though I took a silly, round-about method.
Hope all of this was helpful - or at least interesting!
* And if you're wondering, "Why in the world did you split it in that particular way?" The answer is, "I don't really know. I just had a gut feeling it would be helpful."

