Graphing and Magnitude of Complex Numbers
Reference > Mathematics > Algebra > Complex NumbersSomewhere in the history of complex numbers, some mathematician had a brilliant idea for representing complex numbers graphically. It's brilliant not just because it gives us a way of visualizing complex numbers; it's brilliant because it turns out that this method of graphing complex numbers allows us to tie complex numbers to other fields of study like geometry and trigonometry in some ways that produce very interesting results. Since this unit assumes only a rudimentary Algebra background, we won't delve into the trigonometry. But graphing complex numbers allows us to start talking about the "size" of a complex number, which is a very useful concept.
So here's what we do. First, we draw a number line, going from left to right on our page, and we call it the "real" number line. That's nothing new; you've probably been doing number lines like that since you were in elementary school (and you might have even called it the "real number line," without realizing why it was called that). All the real numbers: -1000, 0, 3, pi, etc. are on this number line.
Now draw a second number line, but make this one go from bottom to top, at right angles to the "real" number line. We'll call this one the "imaginary" number line. Instead of having the real numbers on this number line, we'll have all the imaginary ones: -1000i, 0i, 3i, (pi)i, etc.
The imaginary number line and the real number line intersect at one point: 0 and 0i. After all, 0 and 0i are the same number, right? So it looks like this:
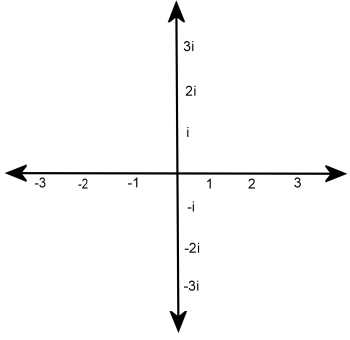
Notice that the positive imaginary values are at the top, and the negative imaginary values are below the real number line. We call these two number lines the "real axis" and the "imaginary axis." We call this graph the "complex plane," and every complex number can be graphed on it.
Suppose we wanted to graph the complex number 2 + 3i. You would go to the right 2 units on the real axis, and up to 3i on the imaginary axis, and mark a point there:

This way of graphing complex numbers gives us a way of talking about how "big" a complex number is. We will say that its size is its distance from the origin (the point 0 + 0i). When you're studying complex numbers, you'll see many different math terms used to describe its size, so it's good to know them all; your teacher will probably have preferred term to use, so ask your teacher about that.
The terms we use to describe the size of a complex number are:
- magnitude
- modulus
- absolute value
"Absolute Value" is an interesting phrase to use, because the absolute value of a real number is its distance from zero on the real number line, so it makes sense that the distance from a complex number to 0 + 0i should be called absolute value. But always remember, what we're really talking about is the size of the complex number.
Finding the size of that complex number 2 + 3i is easy, as long as you remember the Pythagorean Theorem. After all, we can create a triangle like this:
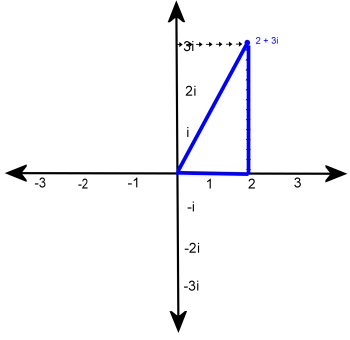
How long are the legs of this triangle? 2 units and 3 units, right? From the origin we went 2 units to the right, and then we went 3 units up, so the legs have lengths 2 and 3. Since the size of this complex number is just the hypotenuse of this triangle, we can use the Pythagorean Theorem to determine the size:
c2 = a2 + b2
c = 22 + 32
22 + 32 13
13This gives us a very simple rule to find the size (absolute value, magnitude, modulus) of a complex number:
|a + bi| = a2 + b2
a2 + b2Note that we've used absolute value notation to indicate the size of this complex number.
Example One
Calculate |3 + 4i|
|3 + 4i| =
 32 + 42
32 + 42 25
25Example Two
Calculate |5 - 12i|
|5 - 12i| =
 52 + (-12)2
52 + (-12)2 25 + 144
25 + 144 169
169Questions
 Multiplying and Dividing Complex Numbers
Multiplying and Dividing Complex Numbers Unit Index
Unit Index

