Factor Trees
Reference > Mathematics > Algebra > FactoringFactor Trees are a visual representation of a number as a combination of its prime factors. They are helpful in determining the prime factorization of a number. The best way of explaining a Factor Tree is to begin with a picture of one:
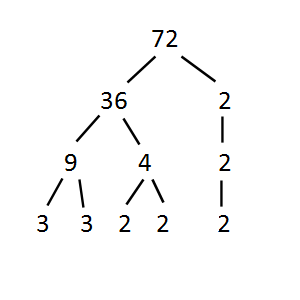
This is a factor tree of the number of 72, and it is developed branch by branch starting from the top. I began by asking myself "What two positive integers multiply together to make 72?" The first thing that popped into my mind was "36 and 2." Maybe you would have thought of "8 and 9" or "12 and 6" instead. It doesn't matter; your factor tree would look different than mine, but in the end we would get the same prime factorization.
Since I thought of 36 and 2, I drew two diagonal lines from the 72 and wrote those two numbers beneath. Then I asked "What two positive integers multiply to make 36?" and I thought of "9 and 4". So I drew branches for these numbers.
Now, you notice that 2 next to the 36? I have to ask myself, "What two positive integers multiply to make 2?" But the answer to that question is, "the only way to make 2 is 1x2," so 2 can't be broken down any more. So I drew a branch straight down and put the 2 underneath it.
Following that, I split 9 into 3 x 3, and 4 into 2 x 2.
Finally, we can use this information to get the prime factorization of 72. At the bottom of our factor tree we have 3 twos, and 2 threes. How do we write that?
Simple! 23 x 32
Remember I said that you'd get the same result even if you split the numbers differently? Here's another possible tree: I could have split 72 into 8 x 9, then split 8 into 4 x 2, and 9 into 3 x 3, then split 4 into 2 x 2. When we're done, we still have 23x 32!
By the way, I always start with the smaller prime factors and work my way up to larger ones when I write my answer. It's just less confusing that way.
Questions
 Unit Index
Unit Index Greatest Common Factor
Greatest Common Factor

