One of my friends shared the following picture on Facebook this morning. He didn't specifically ask me for an answer, but I thought it would be a fun question to explore.

So let's start by asking a question: If it wasn't zero degrees, how would you figure out "twice as cold?" Did you say, "Multiply the temperature by two?"

So, for example, if the temperature was -10 degrees, twice as cold would be -20 degrees?

That seems like it might be a reasonable answer at first glance, except it clearly doesn't work that way, if you just ask this:

If the temperature was 40 degrees, what is twice as cold as that? Now multiply 40 by 2 and you get 80 degrees, which is clearly not colder!

So multiplying the temperature by two doesn't do what we want.

In addition to this, we have another issue with the question: temperature doesn't measure cold. It measures heat. In the same way that we don't measure darkness; we measure light. Amount of light is measured in lumens, and darkness is the absence of light. Cold is not a measured quantity; it is the absence of heat. So saying "twice as cold" may not have any actual meaning to begin with!

The next question to consider is: what scale are you using? Fahrenheit? Celsius? Because that must make a difference too. 0 degrees Celsius is the same as 32 degrees Fahrenheit, and multiplying the first number by 2 gives you zero, while multiplying the second number by 2 gives 64!

Having asked those questions, let's take a break from temperatures and talk about marketing and sales.

I know, I know, that has nothing to do with temperature. Bear with me, though, because I'll get back to temperature in a minute.

Suppose I was hired by a firm to do marketing and sales work. I was hired at the beginning of 2015, and at the end of the year, I wanted to impress my bosses with how much I'd helped the company's bottom line. So I show my boss this chart:

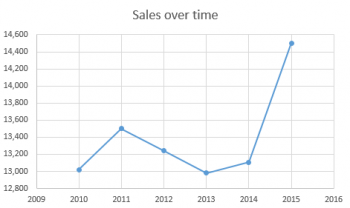
It looks pretty impressive, doesn't it? My boss, if he's not paying attention, will say, "Wow! Look at how much higher the 2015 number is! You've quadrupled our sales, just in one year!"

But if he's paying attention carefully, he'll say, "Wait a minute! Why does your chart's axis start at $12,800 instead of $0?

And the answer is...if my chart started at zero, my bosses wouldn't be nearly as impressed with me:

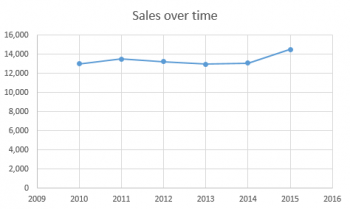
You see, once we have a frame of reference for comparison, we realize that the difference between the 2015 number and the 2014 number isn't nearly as big as it looked in the first chart. And I certainly didn't quadruple their sales, even though it looked like it in the first chart.

The same is true with temperatures: if you want to make comparisons like "twice" or "half," you really need to have a "real" zero. Zero on the Celsius scale doesn't actually "mean" zero, because zero should mean "no heat at all" (just like zero on my sales chart means "no sales at all"). We need to have a scale in which zero really means "no heat whatsoever."

Fortunately, we have a scale like that. It's the Kelvin scale, in which zero is called "absolute zero" because it is the end of the line. There is no heat whatsoever at zero Kelvin. In the Kelvin scale, 0 Kelvin is equal to -273.16 degrees Celsius, and 273.16 Kelvin is equal to 0 degrees Celsius.

Okay, so now let's make some assumptions. Let's suppose that the guy in the picture means 0 degrees Celsius. Let's also suppose that when he says "twice as cold" he really means "half as much heat energy."

If we make those two assumptions, then we can do the following:

0 degrees Celsius = 273.16 Kelvin

Half of 273.16 Kelvin is 136.58 Kelvin

And 136.58 Kelvin is equal to -136.58 degrees Celsius.

There ya go. If the temperature is 0 (assuming Celsius scale), and it's going to be twice as cold tomorrow, it'll be -136.58 degrees Celsius tomorrow. Of course, we had to make some assumptions along the way, but at least we have an answer!