B. from Vermont wants to know what "cis" notation is, how it works, and why it's useful.

"cis" is a shorthand way of writing complex numbers. Let's talk for just a minute about what complex numbers are. If you're already familiar with complex numbers, you can skip to the next section.

Complex Numbers

A complex number is a number which is made up of two parts. The first part is called the "real" part, and it is a real number (any of your normal counting numbers, zero, negatives, fractions, radicals, etc.) and the second part of the number is a real number times i.

i, in case you don't know, is the square root of negative one. "But," you might protest, "that's not a real number!" That's correct. In a very literal sense, by definition, it is not a member of the set of Reals.

So a complex number looks like this. a + bi. We call the "a" the "real part" and "b" is the "imaginary part."

Graphing Complex Numbers

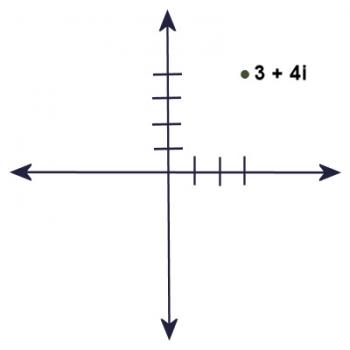
Obviously, you can't graph a complex number on a number line, since the number line contains only Real numbers. However, if you take two number lines and put them at right angles to each other, so that they cross on their zeroes, you can now graph a complex number. You use the horizontal number line to measure off the real part, and you use the vertical number line to measure off the imaginary part.

So, for example, to graph the point 3 + 4i, we would count three units to the right, and 4 units up. It's the same process we would use to graph the ordered pair (3,4) on a cartesian plane.

Similarly, -3 +4i would be graphed like this: count three units to the left, and four units up.

Magnitude and Angle

I don't know if you've ever thought about this, but if you're graphing points on a cartesian plane, every point can be described with an x and y, but there is another way to describe the point. You can describe it using a magnitude and an angle.

The magnitude is its distance from the origin (0,0), and its angle is the angle it makes with the positive x axis.

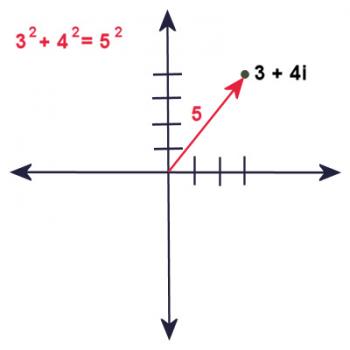
In the same way, every complex number can be described using a magnitude and angle. Let's consider the complex number 3 + 4i.

How far is that point from the origin? Well, it's three units right and four units up. Using the Pythagorean Theorem (or the distance formula, which is basically the same thing), we find that its distance from the origin is the square root of (3² + 4²), which is 5 units.

so r = 5.

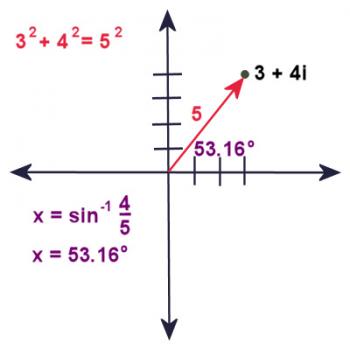
But what about the angle? Well, if you've done some trig, you'll figure out that the angle is sin^-1(4/5), which is approximately 53.16 degrees.

In the same way, you could find an angle and radius for every complex number on the plane.

CIS Notation

But wait a minute! Doesn't that mean we can write 3 + 4i like this: 5(cos(53.16º) + isin(53.16º))?

As a matter of fact, it does mean that. Every complex number can be written in the form r(cosx + isinx), where r is the complex number's magnitude, and x is its angle.

Mathematicians are notorious for not wanting to write everything out longhand, so, cosx + isinx gets simplified to CIS, which stands for "Cosine i Sine".

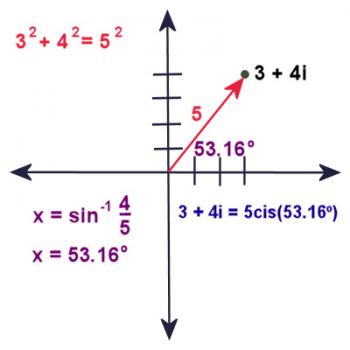
So 3 + 4i can be written as 5cis53.16º

That, hopefully, will answer your question "What is cis notation?" CIS notation is a shorthand way of writing complex numbers using its magnitude and some trig functions.