This question comes from one of my Pre-Cal students, who wants to know if there's a nice rule like the "sum and product" factoring rule, that works when the roots are complex numbers.

The sum-and-product method he's referring to is this:

If we have a quadratic x² + bx + c, and we can find two numbers (let's call them m and n) that add to b and multiply to c, then the quadratic factors into (x + m)(x + n). Here's an example:

Factor x² + 13x + 36.

In order to factor this, I look for two numbers that add to 13, and multiply to 36. Can you find them? I usually start by asking, "What are two numbers that multiply to 36?" The first pair I think of is 6 x 6. But 6 + 6 isn't 13, so that doesn't work. Next I think of 9 x 4. Aha! 9 + 4 is 13. So, since 9 x 4 = 36 and 9 x 4 = 13, I conclude that:

x² + 13x + 36 = (x + 4)(x + 9).

Okay, so now the question is, what if the quadratic factors with complex numbers? Is there a nice way of doing this factoring rule?

Let's start with an example:

x² - 4x + 5

If I knew that the factorization of this resulted in complex numbers, I would remember another rule, that complex roots come in pairs: if one root is a + bi, then the other is a - bi.

So, we look for two numbers such that:

(a + bi) + (a - bi) = -4
(a + bi)(a - bi) = 5

Simplifying these gives:

2a = -4, or a = -2
a² + b² = 5
4 + b² = 5
b² = 1
b = ⁺/_- 1

Therefore, this factors as follows:

x² - 4x + 5 = (x - 2 - i)(x - 2 + i) Multiply this out, and sure enough, it's true.

Let's try generalizing this a bit. Suppose the quadratic was x² + mx + n, and we wanted to find complex roots with the sum and product method.

(a + bi) + (a - bi) = m
(a + bi)(a - bi) = n

2a = m
a² + b² = n

a = m/2

m²/4 + b² = n
b = SQR(n - m²/4)

So let's take another example, and put our rule into practice.

x² + 6x + 13

a is half of 6, or 3.

b is SQR{13 - 6²/4) = SQR{13 - 9} = 2.

Therefore x² + 6x + 13 = (x +3 + 2i)(x + 3 - 2i).

This isn't too bad, but it presumes that the leading coefficient of the quadratic is 1; things might get a bit dicier if it wasn't. And, of course, if you're paying close attention, the result we obtain is actually just a slightly re-arranged version of the quadratic formula as it would appear in the special case of the leading coefficient being one!

In our previous blog post, we were answering the question "Why is it useful to write complex numbers in trigonometric form?"

We saw how squaring a complex number can be simplified using trig, and we saw the same thing is true for multiplying any two complex numbers. In this blog post we'll explore how trigonometric form for complex numbers can help us take roots (cube roots, fourth roots, etc).

Before we get into taking roots of numbers, I'd like to point out something that you might not have realized: there are an infinite number of ways to write a complex number in cis form, because cos and sin are periodic functions:

rcis(xº) = rcis(xº + 360º) = rcis(xº + 720º) = etc.

Okay, tuck that information away in your memory banks; we'll get back to it shortly. Now let's talk about taking a cube root.

Let's suppose we wanted to take the cube root of the number 8...

"Well, that's silly," you might argue, "I already know the cube root of 8. It's TWO!"

Ah...but you only think you know. Bear with me, and I'll show you something interesting.

How would you write 8 as a complex number? It's 8 + 0i. Which is the same as 8cis0º. Now we know from the previous post, that if rcisx cubed equals 8cis0º, then r³ = 8, and 3x = 0º. Or, since it's the same value, 3x = 360º, or 3x = 720º.

Thus, x = 0º, x = 120º, or x = 240º.

Therefore, the cube roots of 8cis0º are 2cis0º, 2cis120º,  and 2cis120º.

But what are those numbers?

Well, 2cis0º is easy; it's just 2 + 0i = 2. "Ah ha!" you might say, "I told you it was two!"

Very good, but let's keep going:

2cis120º = 2cos120º + 2isin120º = -1 + 1.732i

2cis240º = 2cos240º + 2isin240º = -1 - 1.732i

So it turns out that 8 has three cube roots, and you found them using trigonometry!

It turns out that you could have found those roots algebraically, by setting up the following equation:

x³ = 8

x³ - 8 = 0

(x - 2)(x² + 2x + 4) = 0

So either x - 2 = 0 or x² + 2x + 4 = 0

The first equation gives us the root we expected: x = 2.

The second equation can be solved using the quadratic formula:

x = (-2 +/- 3.4641i)/2, which simplifies to:

x = -1 + 1.732i or x = -1 - 1.732i

We obtain the same result algebraically as we did using trigonometry. You might argue that it was easier to use the algebraic method, but that's only because you know how to factor x³ - 8, and the factors are a linear factor and a quadratic. But suppose I'd asked you to find the fifth root of 32...what would you have done then? Or what if I'd asked you to find the cube root of 1 - 2i?

In these cases, algebraic solutions would be much more challenging, and the the trigonometry solution simplifies the process significantly.

This is a follow-up post to yesterday's "What is CIS Notation?" post. In this post we explore why it is useful to write complex numbers in their trigonometric form. Here you will find reference to the trigonometric double-angle formulas, and sum-of-angle formulas. If you're not familiar with these, you'll just have to take our word for those steps!

Let's start with a complex number in trigonometric form: 4cis(30º). If we were to write this number out without using the "cis" shorthand, it would look like this:

4[cos(30º) + isin(30º)]

This evaluates to approximately 3.4641 + 2i

Now supposing we wanted to square this complex number. You know the process, right?

(3.4641 + 2i)² =

(3.4641 + 2i)(3.4641 + 2i) =

12 + 6.9282i + 6.9282i - 4 = 

8 + 13.8564i

Let's do the same thing, but using the trig form for the complex number.

{4[cos(30º) + isin(30º)]}² =

4[cos(30º) + isin(30º)] · 4[cos(30º) + isin(30º)] = 

16[cos²(30º) + isin(30º)cos(30º) + isin(30º)cos(30º) - sin²(30º)] = 

16[cos²(30º) - sin²(30º) +2isin(30º)cos(30º)] = 

Now here's where those double-angle formulas come in:

cos(2x) = cos²(x) - sin²(x)

sin(2x) = 2sin(x)cos(x)

Thus, our expression can be simplified to:

16[cos(60º) +isin(60º)] = 

16cis(60º)

Do you see what just happened there? When all is said and done, we ended up squaring the magnitude, and doubling the angle, and that was it!

As another example, let's take the complex number that we used in our previous blog post: 3 + 4i. If you wanted to square this, you would multiply it out as follows:

(3 + 4i)(3 + 4i) = 

9 + 12i + 12i - 16 = 

-7 + 24i

On the other hand, if we had the angle in cis notation: 5cis(53.16º), we can square the complex number by squaring the magnitude, and doubling the angle:

5cis(53.16º) = 25cis(106.32º), and we're done, just like that! That was a LOT quicker!

And, incidentally, this works for any cubing, raising to the fourth power, etc. To raise a complex number to the n^th power, raise its magnitude to the n^th, and multiply its angle by n. Now that's "power"ful! 

But suppose we aren't squaring a complex number - suppose we're multiplying two different complex numbers? What happens then?

Let's make this very general; we'll call the two complex numbers r₁cisA and r₂cisB. Their product is:

r₁(cosA + isinA) · r₂(cosB + isinB) = 

r₁r₂(cosAcosB + icosAsinB + isinAcosB - sinAsinB) = 

r₁r₂[(cosAcosB - sinAsinB) +  i(cosAsinB + sinAcosB)] =

r₁r₂[cos(A + B)* +  isin(A + B)*] =

r₁r₂cis(A + B)

* sum of angle formulas were used to obtain this result.

Wow! Isn't that a great result - to multiply two complex numbers, you multiply their magnitudes and add their angles! That's easy!

But the real power (that was a double pun, by the way) of this way of writing complex numbers is in taking roots of numbers.

And that, I think, will become the topic of one more follow-up blog post!

B. from Vermont wants to know what "cis" notation is, how it works, and why it's useful.

"cis" is a shorthand way of writing complex numbers. Let's talk for just a minute about what complex numbers are. If you're already familiar with complex numbers, you can skip to the next section.

Complex Numbers

A complex number is a number which is made up of two parts. The first part is called the "real" part, and it is a real number (any of your normal counting numbers, zero, negatives, fractions, radicals, etc.) and the second part of the number is a real number times i.

i, in case you don't know, is the square root of negative one. "But," you might protest, "that's not a real number!" That's correct. In a very literal sense, by definition, it is not a member of the set of Reals.

So a complex number looks like this. a + bi. We call the "a" the "real part" and "b" is the "imaginary part."

Graphing Complex Numbers

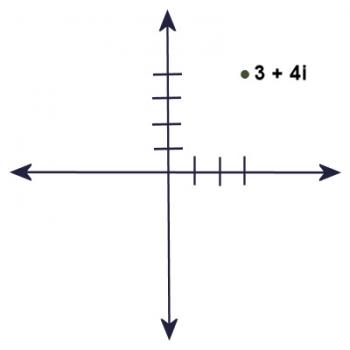
Obviously, you can't graph a complex number on a number line, since the number line contains only Real numbers. However, if you take two number lines and put them at right angles to each other, so that they cross on their zeroes, you can now graph a complex number. You use the horizontal number line to measure off the real part, and you use the vertical number line to measure off the imaginary part.

So, for example, to graph the point 3 + 4i, we would count three units to the right, and 4 units up. It's the same process we would use to graph the ordered pair (3,4) on a cartesian plane.

Similarly, -3 +4i would be graphed like this: count three units to the left, and four units up.

Magnitude and Angle

I don't know if you've ever thought about this, but if you're graphing points on a cartesian plane, every point can be described with an x and y, but there is another way to describe the point. You can describe it using a magnitude and an angle.

The magnitude is its distance from the origin (0,0), and its angle is the angle it makes with the positive x axis.

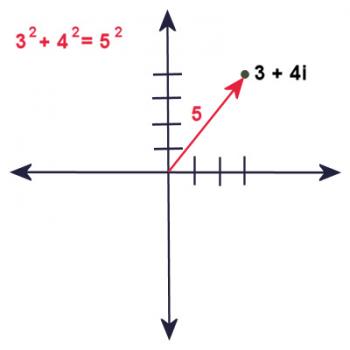
In the same way, every complex number can be described using a magnitude and angle. Let's consider the complex number 3 + 4i.

How far is that point from the origin? Well, it's three units right and four units up. Using the Pythagorean Theorem (or the distance formula, which is basically the same thing), we find that its distance from the origin is the square root of (3² + 4²), which is 5 units.

so r = 5.

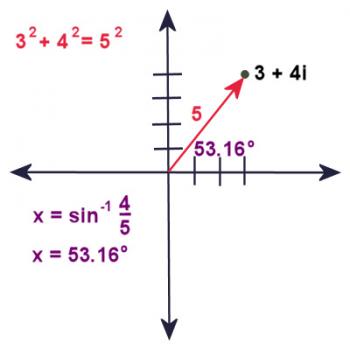
But what about the angle? Well, if you've done some trig, you'll figure out that the angle is sin^-1(4/5), which is approximately 53.16 degrees.

In the same way, you could find an angle and radius for every complex number on the plane.

CIS Notation

But wait a minute! Doesn't that mean we can write 3 + 4i like this: 5(cos(53.16º) + isin(53.16º))?

As a matter of fact, it does mean that. Every complex number can be written in the form r(cosx + isinx), where r is the complex number's magnitude, and x is its angle.

Mathematicians are notorious for not wanting to write everything out longhand, so, cosx + isinx gets simplified to CIS, which stands for "Cosine i Sine".

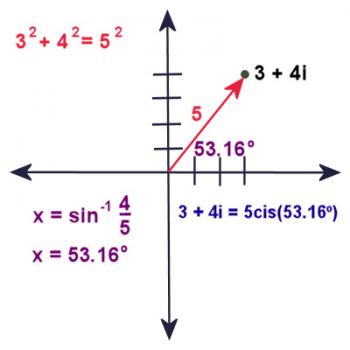
So 3 + 4i can be written as 5cis53.16º

That, hopefully, will answer your question "What is cis notation?" CIS notation is a shorthand way of writing complex numbers using its magnitude and some trig functions.