Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Bianca, an 11th grader from Canada asks, "Hello, I need help in math, how can I prove that the cosine of 36 is equal to the number of gold divided by 2."
That's a great question, Bianca. For anyone who doesn't know, the "number of gold" or "the golden ratio" is the number (1 + SQR(5))/2, which is approximately 1.6180339887. This number is interesting largely because the Greeks were fascinated by it, and because certain sequences which appear in nature sort of "zero in" on this number.
So how do we prove that the cosine of 36 degrees is this magical number? Well, we'll start by drawing a picture of an isosceles triangle which has angles 36-72-72.

Let's add a line segment to this triangle; let's add an angle bisector from angle B to the opposite side.

This produces some interesting similarities and congruences. For starters, measure of angle DBC is half of the measure of angle ABC, or 36º. Since the measure of angle DCB is 72º, we have triangle ABC similar to triangle BDC, and BC = BD (because the triangle is isosceles).
We can use some similar reasoning on triangle ABD to conclude that it is also an isosceles triangle, with BD = DA.
Putting all of this together leads to BC = BD = DA.
Now, since triangle ABD is similar to triangle BCD, we can conclude that
AC / BC = BC / CD
BC2 = (AC)(CD)
Now we can do a substitution, by noting that AC = AD + DC which equals BC + DC.
BC2 = (BC + DC)(DC)
BC2 = (BC)(DC) + DC2.
At this point, I'd like to do two things to this equation. First, I'd like to divide both sides by DC2, and then I'd like to do a substitution: x = BC/DC. This results in the following equation:
x2 - x - 1 = 0.
This can be solved using the quadratic formula: x = (1 + SQR(5))/2, or the golden ratio!
But how do we get here from to the trig function you want? Well, for starters, since the larger triangle is similar to the smaller one, we also have AB/BC = the golden ratio.
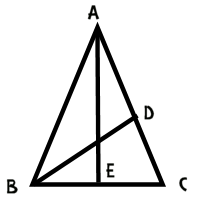
Now if we draw a perpendicular down the middle of the diagram, we've got AB/BE = 1/2 of AB/BC, or half of the golden ratio. This means that BE/AB is 1/2 of the golden ratio. But BE/AB is the cosine of 72 degrees, since AEB is a right triangle.
Thus, cos(72º) = 2/x, where x is the golden ratio.
From here we can use a half angle identity:
cos(36º) = SQR((1 + cos(72º))/2)
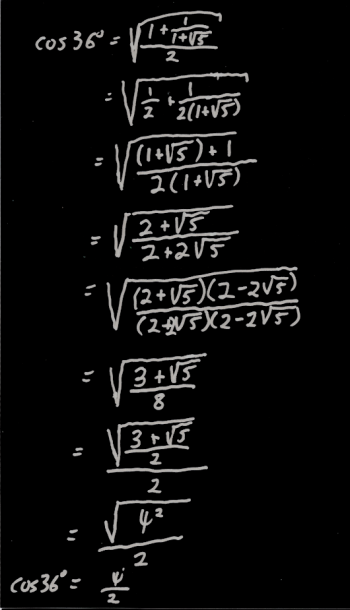
Now if you think that looks ugly, you're right. If you punch it into your calculator, you'll find that it evaluates to 0.809016994, which is half of the golden ratio. However, it would be nice to have an algebraic proof, right?
I worked through the algebra, but typing it all out on the blog would be UGLY, so I'm just going to post an image of the work I did on paper.
To view a larger version of this image, just click on it.
When I got to the end of the algebra, I had a radical within a radical, which is an ugly looking beast, but I happened to remember that (3 + SQR(5))/2 is the square of the golden ratio, which made the whole thing simplify quickly.
Is there an easier way to arrive at the cos(36º)? I'm sure there is. This was just the first one that came to mind. There might be other ways to do this using the law of cosines, or the law of sines, and I know you can do it with an entirely non-geometric proof (using various trig identities) but this one does the job. If you find a simpler proof, let me know!


