From Amber: "I'm trying to figure out the angle of a set of stairs using a scalene triangle basically you have a 90 degree angle one side is 8 feet and one is 3.5 feet what would be the slope or the angle of the third side"

Hi Amber. You didn't state in your question whether 8 feet is the horizontal length of the staircase and 3.5 feet the height? Or perhaps 8 is the length along the slope of the staircase? Of course, that makes a difference, so I'll help you work it out both ways.

First, as you pointed out, you have a right triangle. If the 8 and 3.5 are the legs of the triangle, that's all you need.

However, if 8 is the hypotenuse, you need to use the Pythagorean Theorem to find the missing side length: x² = 8² - 3.5². Which leads to x = 7.2 (approximately)

There are two basic rules that you need to know. The first rule is that the slope is "rise over run." In other words, it's the amount that the staircase rises divided by the amount the staircase goes horizontally. So if the staircase is 8 feet horizontally and 3.5 feet vertically, the slope is 3.5 / 8 = 0.4375. On the other hand, if the horizontal length is 7.2, the slope is 3.5 / 7.2 = 0.4861.

Okay, so now you need the second rule, which is that the slope is the slope is the same as the tangent of the angle. Or, to put it a little differently, the angle is the inverse tangent of the slope.

You probably know how to do trig functions on your calculator, but in case you don't, on most calculators, you'll get the inverse tangent function by pressing "2nd" (or "Shift") and then the "TAN" button. So you'll press 2nd  TAN  0.4375 = 23.6 degrees. Or, if we're using the second possibility, 2nd TAN 0.4861 = 25.9 degrees.

In either case, that's a fairly shallow angle for stairs; I think the "standard" (at least in the US) is closer to 30 degrees than 25 degrees.

Hopefully that helps out - thanks for asking!

One of my Pre-Cal students asked me a few days ago if the Law of Sines was hard to prove. I told him I'd write up a proof here. I also made my Pre-Cal class work through the proof themselves. I'll share their train of reasoning here.

First, we stated the Law of Sines:

in triangle ABC, a/sinA = b/sinB = c/sincC.

They quickly recognized that we need a diagram to work from. So we drew something like the diagram to the right.

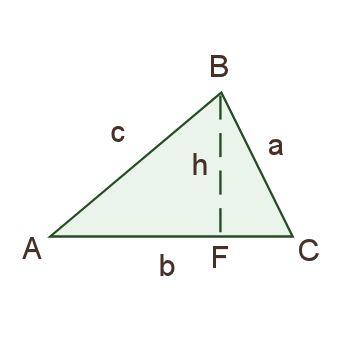
Then one of the students said, "Maybe we should draw in an altitude." Thus we had the following diagram. Their choice to label that new point F was somewhat random, I think, but I liked it, because F can stand for "foot" of the altitude.

After puzzling over their diagram for a bit, someone suggested setting up an equation involving the sine function and triangle ABF, and after a bit more thinking, a second equation involving the sine function and triangle CBF:

sinA = h/c; sinC = h/a.

They then did one of their favorite algebraic steps: multiplying both sides of an equation by a denominator in order to get rid of fractions (they don't like fractions, so they're always happy to get rid of them):

csinA = h; asinC = h.

A little substitution gives csinA = asinC. They then chose to divide both sides of this equation by sinAsinC, which gives:

c/sinC = a/sinA.

At this point, someone said, "Well we can just do this all over again with another side." Sure enough, if you drew an altitude to a different side, you'd get b/sinB = c/sinC (or b/sinB = a/sinA, depending on which altitude you drew).

Thus, a/sinA = b/sinB = c/sinC, and the Law of Sines is proved. Nice teamwork, class!

Bianca, an 11th grader from Canada asks, "Hello, I need help in math, how can I prove that the cosine of 36 is equal to the number of gold divided by 2."

That's a great question, Bianca. For anyone who doesn't know, the "number of gold" or "the golden ratio" is the number (1 + SQR(5))/2, which is approximately 1.6180339887. This number is interesting largely because the Greeks were fascinated by it, and because certain sequences which appear in nature sort of "zero in" on this number.

So how do we prove that the cosine of 36 degrees is this magical number? Well, we'll start by drawing a picture of an isosceles triangle which has angles 36-72-72.

Let's add a line segment to this triangle; let's add an angle bisector from angle B to the opposite side.

This produces some interesting similarities and congruences. For starters, measure of angle DBC is half of the measure of angle ABC, or 36º. Since the measure of angle DCB is 72º, we have triangle ABC similar to triangle BDC, and BC = BD (because the triangle is isosceles).

We can use some similar reasoning on triangle ABD to conclude that it is also an isosceles triangle, with BD = DA.

Putting all of this together leads to BC = BD = DA.

Now, since triangle ABD is similar to triangle BCD, we can conclude that

AC / BC = BC / CD

BC² = (AC)(CD)

Now we can do a substitution, by noting that AC = AD + DC which equals BC + DC.

BC² = (BC + DC)(DC)

BC² = (BC)(DC) + DC².

At this point, I'd like to do two things to this equation. First, I'd like to divide both sides by DC², and then I'd like to do a substitution: x = BC/DC. This results in the following equation:

x² - x - 1 = 0.

This can be solved using the quadratic formula: x = (1 + SQR(5))/2, or the golden ratio!

But how do we get here from to the trig function you want? Well, for starters, since the larger triangle is similar to the smaller one, we also have AB/BC = the golden ratio.

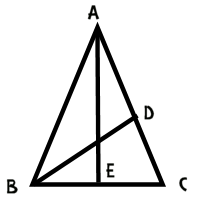
Now if we draw a perpendicular down the middle of the diagram, we've got AB/BE = 1/2 of AB/BC, or half of the golden ratio. This means that BE/AB is 1/2 of the golden ratio. But BE/AB is the cosine of 72 degrees, since AEB is a right triangle.

Thus, cos(72º) = 2/x, where x is the golden ratio.

From here we can use a half angle identity:

cos(36º) = SQR((1 + cos(72º))/2)

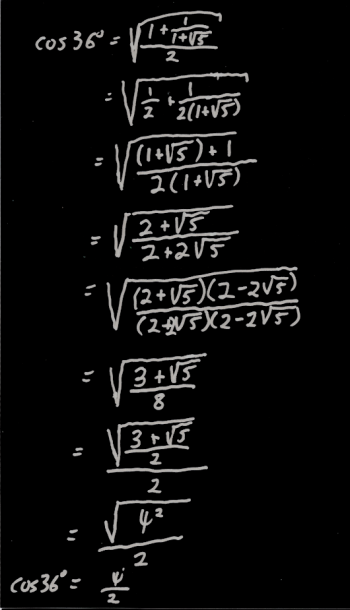
Now if you think that looks ugly, you're right. If you punch it into your calculator, you'll find that it evaluates to 0.809016994, which is half of the golden ratio. However, it would be nice to have an algebraic proof, right?

I worked through the algebra, but typing it all out on the blog would be UGLY, so I'm just going to post an image of the work I did on paper.

To view a larger version of this image, just click on it.

When I got to the end of the algebra, I had a radical within a radical, which is an ugly looking beast, but I happened to remember that (3 + SQR(5))/2 is the square of the golden ratio, which made the whole thing simplify quickly.

Is there an easier way to arrive at the cos(36º)? I'm sure there is. This was just the first one that came to mind. There might be other ways to do this using the law of cosines, or the law of sines, and I know you can do it with an entirely non-geometric proof (using various trig identities) but this one does the job. If you find a simpler proof, let me know!