Question: In your Gravity Train Simulator, you made the following statement: "If the train is inside the earth, the force of gravity acting on it is related not just to its distance from the center of the earth, but also on the amount of earth mass which is closer to the center of the earth than the train is." This seems to imply that all the mass outside the train's radius somehow cancels out. So if someone was in outer-space, inside an enormous steel shell - does that mean they would be weightless wherever they were in the shell? ~H. Borash

Answer: Yes, that's correct, H. To rigorously prove this, we would need to use a bit of Calculus, but I can show you a rough geometry approximation that'll help you see why it's true. First, a diagram. Here's a spherical shell. We'll assume it's absolutely enormous - big enough to enclose the earth and the sun. This hypothetical structure is called a Dyson sphere. I've marked the sun and the earth inside the sphere.

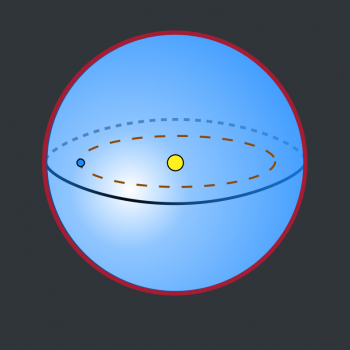
The yellow circle at the center of the sphere represents the sun, and the smaller blue circle to the left represents the earth. The brown dotted line represents the earth's orbit around the sun.

Obviously, this is not drawn to scale; it's difficult to make both the sun and earth to scale in a single diagram without the earth becoming nearly invisible. So I didn't even try.

But the question you asked is essentially equivalent to this: wouldn't the Dyson sphere throw the earth out of its orbit? That sphere has got to be incredibly massive, and planet earth is much closer to one side than the other. So wouldn't earth get dragged out of its orbit?

Or, to put it another way, if the sun wasn't there at all, and earth was motionless, would it stay motionless? Or would it get dragged toward the closer side of the sphere?

The answer to both questions is: No. No, the sphere would not drag the earth out of its orbit. No, earth would not go crashing into the sphere. All of the gravitational forces applied by the sphere on planet earth cancel each other out. Even though earth is not at the center of the sphere.

The reason is that because the earth is closer to one side, there is more mass on the other side, and the closeness of the mass on one side exactly cancels against the extra mass on the other side!

As I said above, a full, rigorous proof of this involves some Calculus, but I'm going to try to give you a non-calculus explanation that may help you visualize what's happening. I want to focus on two disks of the sphere - one close to the earth, and the other on the opposite side, furthest away from earth. To simplify, we're going to treat these as flat disks, so they don't exactly match the contour of the Dyson sphere:

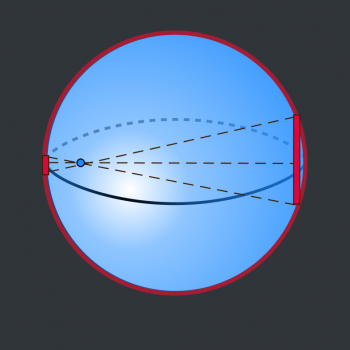
Notice how much bigger the disk on the right is, compared to the one on the left. That disk is much further away, so each cubic inch of that disk exerts less force on earth than a corresponding cubic inch of the closer disk.

On the other hand, you can easily see that the disk on the right contains many many more cubic inches than the disk on the left.

So maybe they cancel? Let's take a closer look.

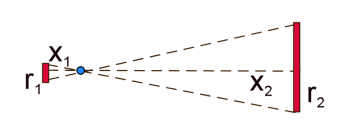
If we knew the thickness (h, for height) of the disk, as well as the density (D) of the material the disk is made of, we could calculate the masses (m₁ and m₂) of the two disks.

m₁ = hπr₁²D

m₂ = hπr₂²D

However, we have more variables than we need. Since we have some similar triangles, we can say that r₂ = r₁(x₂/x₁). This changes our second equation to: m₂ = hπr₁²(x₂²/x₁²)D.

Now this is where the magic happens: we're going to plug both of those masses into the gravitational formula:

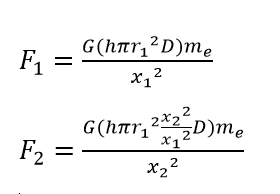
So even though one disk is much larger than the other, they both exert the same gravitational force on earth, canceling each other out!

Again, this is not a rigorous proof. Most proofs I've seen of this involve rings instead of disks, and doing integrals (calculus) to show that all the rings cancel. But this geometric demonstration hopefully helps you to see that it's a reasonable conclusion!