Happy Valentine's Day, one day late! We hope you all had a wonderful day yesterday, no matter how (or if) you celebrated the day. For all of our online friends, I have the only Valentine's Day card you'll ever need for your mathematician friends.

It references counting principles in combinatoric mathematics, and in case you're not familiar with the notation, please allow me to explain.

Suppose you went to a pizza restaurant, and when you ordered your pizza, they told you, "You can choose from any of the following toppings: pepperoni, olives, hamburg, mushrooms, onions, ham, pineapple, or sausage. Of those, you must choose three toppings." (I know, what restaurant demands that you choose exactly three toppings?)

So how do you determine the number of possible pizzas? Well, the reasoning goes something like this:

1. I have eight ways to choose the first topping (because there are eight toppings available).
2. Once I've done that, I now have seven ways to choose the second topping (because I've already chosen one).
3. Now for my third topping, I have six choices.
4. That gives me 8 x 7 x 6 = 336 possibilities.
5. BUT WAIT A MINUTE! If I chose "pepperoni, olives and ham" - is that really any different from choosing "olives, ham, and pepperoni"?? No, it's not; it's the same pizza no matter what order I pick the toppings in. So I have to eliminate the repetitions.
6. It turns out the number of repetitions is 6. Why? Because you could put pepperoni in 3 positions, leaving 2 positions for olives, and then 1 position for ham. 3 x 2 x 1 = 6.
7. So we take the total number of possibilities (336) and, recognizing that every different pizza has been counted six times, we divide by 6: ³³⁶/₆ = 56. There are 56 different ways of choosing your pizza.

There's a nice way of representing the fact that we've got 8 things to choose from, aned we're choosing 3 of them, and it looks like this:

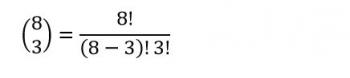
But how do we read that funny notation with the parentheses and two numbers inside of it? Since there are eight things, and we are choosing three, we read it as follows: "Eight choose three."

So, in honor of Valentine's Day, be sure to tell your favorite mathematician: